Točno
25. siječnja 2015. 11:58 (11 godine, 1 mjesec)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Mora vrijediti sljedece:
n > 3 (jer je to n-terokut)
n*alfa < 180 (jer je to najveci kut u tom mnogokutu, a svi kutevi u konveksnom mnogokutu moraju biti manji od 180)
alfa+2*alfa+3*alfa+...+n*alfa=(n-2)*180 (zbroj kuteva u mnogokutu)
|
|
|
v
(1+2+3+...+n)*alfa=(n-2)*180
n*(n+1)*alfa=(n-2)*360
alfa=(n-2)*360/(n*(n+1))
n*alfa < 180
n*(n-2)*360/(n*(n+1)) < 180
(n-2)*2/(n+1) < 1
(2n - 4 - n - 1)/(n+1) < 0
(n - 5)/(n+1) < 0 (smijem jer je n>3, pa je n+1 sigurno vece od 0)
n-5<0
n<5
Rjesenja su n e {3,4}.
n > 3 (jer je to n-terokut)
n*alfa < 180 (jer je to najveci kut u tom mnogokutu, a svi kutevi u konveksnom mnogokutu moraju biti manji od 180)
alfa+2*alfa+3*alfa+...+n*alfa=(n-2)*180 (zbroj kuteva u mnogokutu)
|
|
|
v
(1+2+3+...+n)*alfa=(n-2)*180
n*(n+1)*alfa=(n-2)*360
alfa=(n-2)*360/(n*(n+1))
n*alfa < 180
n*(n-2)*360/(n*(n+1)) < 180
(n-2)*2/(n+1) < 1
(2n - 4 - n - 1)/(n+1) < 0
(n - 5)/(n+1) < 0 (smijem jer je n>3, pa je n+1 sigurno vece od 0)
n-5<0
n<5
Rjesenja su n e {3,4}.
Ocjene: (1)
Komentari:
ikicic, 25. siječnja 2015. 17:35
 Školjka
Školjka 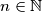 postoje kut
postoje kut  i konveksan
i konveksan  -terokut s kutovima
-terokut s kutovima 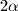 ,
,  ,
, 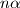 ?
? 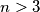 umjesto
umjesto 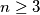 .
.