Točno
2. svibnja 2012. 20:46 (13 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavljam da je pitanje može li se svaki niz realnih brojeva rastaviti na konačno mnogo monotonih nizova.
Nije moguće. Promatrajmo sljedeći niz:
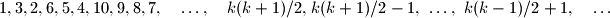

Odnosno, sastavimo niz izvrtanjem i spajanjem konačnih nizova ,
, 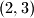 ,
, 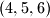 ...
... 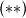
Pretpostavimo da postoji rješenje, tj. traženi konačan skup od rastućih i
rastućih i  padajućih nizova.
padajućih nizova.
Svaki padajući niz može imati samo konačno mnogo elemenata (čini podniz samo jednog sastavnog niza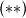 ). Dakle, rastući nizovi moraju pokriti skoro sve elemente početnog niza
). Dakle, rastući nizovi moraju pokriti skoro sve elemente početnog niza  .
.
Promotrimo bilo koji okrenuti niz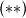 s
s 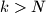 elemenata, takav da ne dijeli niti jedan element s padajućim nizovima (to je moguće jer je
elemenata, takav da ne dijeli niti jedan element s padajućim nizovima (to je moguće jer je  konačan). Svaki od
konačan). Svaki od  rastućih nizova može pokriti samo
rastućih nizova može pokriti samo  element od tog
element od tog  -članog niza (jer je padajuć). Prema tome, ostaju neki nepokriveni elementi, pa ne postoji rješenje.
-članog niza (jer je padajuć). Prema tome, ostaju neki nepokriveni elementi, pa ne postoji rješenje.
Nije moguće. Promatrajmo sljedeći niz:
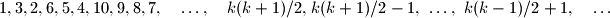

Odnosno, sastavimo niz izvrtanjem i spajanjem konačnih nizova
 ,
, 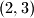 ,
, 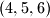 ...
... 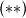
Pretpostavimo da postoji rješenje, tj. traženi konačan skup od
 rastućih i
rastućih i  padajućih nizova.
padajućih nizova.Svaki padajući niz može imati samo konačno mnogo elemenata (čini podniz samo jednog sastavnog niza
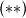 ). Dakle, rastući nizovi moraju pokriti skoro sve elemente početnog niza
). Dakle, rastući nizovi moraju pokriti skoro sve elemente početnog niza  .
.Promotrimo bilo koji okrenuti niz
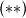 s
s 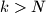 elemenata, takav da ne dijeli niti jedan element s padajućim nizovima (to je moguće jer je
elemenata, takav da ne dijeli niti jedan element s padajućim nizovima (to je moguće jer je  konačan). Svaki od
konačan). Svaki od  rastućih nizova može pokriti samo
rastućih nizova može pokriti samo  element od tog
element od tog  -članog niza (jer je padajuć). Prema tome, ostaju neki nepokriveni elementi, pa ne postoji rješenje.
-članog niza (jer je padajuć). Prema tome, ostaju neki nepokriveni elementi, pa ne postoji rješenje. Ocjene: (1)
Komentari:
grga, 31. kolovoza 2015. 00:58
 Školjka
Školjka