Točno
1. veljače 2015. 00:29 (11 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Da bi neki broj bio djeljiv s 15, mora biti djeljiv s 3 i s 5.
Svaki broj oblika 10^n + 5 je djeljiv s 5 jer je 5 djeljiv s 5 i 10^n je 5^n*2^n, pa je i to djeljivo s 5.
Neka je == znak kongruencije.
10 == 1 (mod 3)
10^n== 1^n==1 (mod 3)
Za svaki n prirodan broj .
5 == 2 (mod 3)
10^n + 5 == 1+2==3==0 (mod 3)
Dakle, zaključak je da to vrijedi za sve prirodne brojeve, odnosno n može biti bilo koji prirodan broj.
Svaki broj oblika 10^n + 5 je djeljiv s 5 jer je 5 djeljiv s 5 i 10^n je 5^n*2^n, pa je i to djeljivo s 5.
Neka je == znak kongruencije.
10 == 1 (mod 3)
10^n== 1^n==1 (mod 3)
Za svaki n prirodan broj .
5 == 2 (mod 3)
10^n + 5 == 1+2==3==0 (mod 3)
Dakle, zaključak je da to vrijedi za sve prirodne brojeve, odnosno n može biti bilo koji prirodan broj.
 Školjka
Školjka 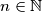 za koje vrijedi
za koje vrijedi 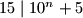 .
.