50%
14. travnja 2012. 20:22 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
recimo da je n neki supersretan broj.
recimo da mu je c broj jedinica, b broj desetica, a a broj stotica.
ako je c <3 onda će n+7, n+6 ili n+5 biti sretan broj i n nije supersretan broj
ali ako je c>3 onda imamo ovo: c+k=10, k<7, tj,; zbroj znamenaka broja n je sada
p mod 7 (pretpostavimo da p nije 0 jer bi onda ovo bio protuprimjer)
onda jedan od brojeva n+12, n+11, n+10, n+9, n+8 ili n+7 biti sretan.
znaci, c=3
no, ako je b<9 onda dolazi do problema:
b+c=7k
b+3=7k /+6
b+9=7k+6 /+1
tu devetka prelazi u deseticu, tj.:
b+10-9=b+1=7k-2
no, dodamo li 2 dobit ćemo:
b+1+2=7k------->b=9
prva znamenka mora biti 9 da bi zbroj znamenaka n+7 bio 1
93 ne uspjeva jer je 95=n+2, a 9+5=14
znači, dodajemo devetke sve dok broj 9...93 ne bude bio djeljiv s 7
prvi koji to ispunjava je 993
n=993
recimo da mu je c broj jedinica, b broj desetica, a a broj stotica.
ako je c <3 onda će n+7, n+6 ili n+5 biti sretan broj i n nije supersretan broj
ali ako je c>3 onda imamo ovo: c+k=10, k<7, tj,; zbroj znamenaka broja n je sada
p mod 7 (pretpostavimo da p nije 0 jer bi onda ovo bio protuprimjer)
onda jedan od brojeva n+12, n+11, n+10, n+9, n+8 ili n+7 biti sretan.
znaci, c=3
no, ako je b<9 onda dolazi do problema:
b+c=7k
b+3=7k /+6
b+9=7k+6 /+1
tu devetka prelazi u deseticu, tj.:
b+10-9=b+1=7k-2
no, dodamo li 2 dobit ćemo:
b+1+2=7k------->b=9
prva znamenka mora biti 9 da bi zbroj znamenaka n+7 bio 1
93 ne uspjeva jer je 95=n+2, a 9+5=14
znači, dodajemo devetke sve dok broj 9...93 ne bude bio djeljiv s 7
prvi koji to ispunjava je 993
n=993
 Školjka
Školjka  "sretan" ako mu je zbroj svih znamenaka višekratnik od
"sretan" ako mu je zbroj svih znamenaka višekratnik od  , i "supersretan" ako je "sretan" i niti jedan od brojeva
, i "supersretan" ako je "sretan" i niti jedan od brojeva 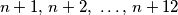 nije "sretan". Koji je najmanji "supersretan" prirodan broj?
nije "sretan". Koji je najmanji "supersretan" prirodan broj?