ikicic, 3. veljače 2015. 21:52
Da, dobiješ sve bodove. Samo moras pokazati da to zbilja je protuprimjer (kao sto si ovdje pokazao, samo sto inace moze biti kompliciranije).
%V0
Da, dobiješ sve bodove. Samo moras pokazati da to zbilja je protuprimjer (kao sto si ovdje pokazao, samo sto inace moze biti kompliciranije).
Zadnja promjena:
Daniel_Sirola, 4. veljače 2015. 12:55
Daniel_Sirola, 3. veljače 2015. 21:12
Ups...
P.S. A za protuprimjer se dobiju svi bodovi?
%V0
Ups...
P.S. A za protuprimjer se dobiju svi bodovi?
Zadnja promjena:
Daniel_Sirola, 3. veljače 2015. 21:26
ikicic, 3. veljače 2015. 19:55
Jesi htio reci da je
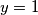
?. Ako da, onda je dobro.
Da, priznat ce ti. Ako je pitanje postavljeno s 'vrijedi li za svaki skup brojeva nesto', a ti nadjes jedam jedini protuprimjer, to ti je dokaz da ta tvrdnja ne vrijedi.
Tu treba napomenuti da nije uvijek lagano naci protuprimjer.
%V0
Jesi htio reci da je $y = 1$?. Ako da, onda je dobro.
Da, priznat ce ti. Ako je pitanje postavljeno s 'vrijedi li za svaki skup brojeva nesto', a ti nadjes jedam jedini protuprimjer, to ti je dokaz da ta tvrdnja ne vrijedi.
Tu treba napomenuti da nije uvijek lagano naci protuprimjer.
Daniel_Sirola, 2. veljače 2015. 23:33
Bi li mi na natjecanju priznali protuprimjer ili treba neko malo objašnjenje ili što da napišem inače kao rješenje?
%V0
Bi li mi na natjecanju priznali protuprimjer ili treba neko malo objašnjenje ili što da napišem inače kao rješenje?
ikicic, 2. veljače 2015. 21:37
Moguce je da je
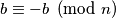
, ako je recimo
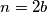
. Tako da ti nije dobro objasnjenje.
No, u ovakvom zadatku ti je sasvim dovoljno naci jedan protuprimjer.
Takodjer, kad se prica o kongruencijama, obicno se misli na cijele brojeve, ne nuzno pozitivne (jer uredjaj i nije pretjerano definiran ili bitan...)
%V0
Moguce je da je $b \equiv -b \pmod n$, ako je recimo $n = 2b$. Tako da ti nije dobro objasnjenje.
No, u ovakvom zadatku ti je sasvim dovoljno naci jedan protuprimjer.
Takodjer, kad se prica o kongruencijama, obicno se misli na cijele brojeve, ne nuzno pozitivne (jer uredjaj i nije pretjerano definiran ili bitan...)
Zadnja promjena:
ikicic, 2. veljače 2015. 21:38
 Školjka
Školjka 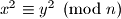 , je li nužno
, je li nužno 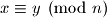 ?
? 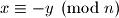 .
.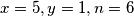 tvrdnja iz zadatka ne vrijedi.
tvrdnja iz zadatka ne vrijedi.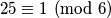 , ali nije
, ali nije 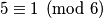 , nego je
, nego je 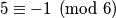
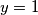 ?. Ako da, onda je dobro.
?. Ako da, onda je dobro.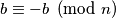 , ako je recimo
, ako je recimo 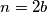 . Tako da ti nije dobro objasnjenje.
. Tako da ti nije dobro objasnjenje.