Točno
3. svibnja 2012. 09:18 (13 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Podijelimo x os na 2011 intervala ovako:
![(-{\infty}, 1], (1, 2], (2, 3], ..., (2009, 2010], (2010, +{\infty}]](/media/m/b/b/8/bb874e46630ddef80498ab7ee6a9d61d.png)
Svakom intervalu pridružimo boju (redom slijeva na desno stavljamo boje od 1 do 2011 )
Promotrimo polinom P(x). Imamo 2 slučaja:
1) Ako njegov graf sječe x os onda ga obojamo bojom intervala njegove najmanje nultočke.
2) Ako graf ne sječe x os onda ga obojamo bojom 2012.
Sve boje smo iskoristili.
Neka su polinomi i
i 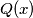 obojani istom bojom.
obojani istom bojom.
Ako oni ne sjeku x os tada niti njihov umnožak ne sječe x os pa su sva tri polinoma obojana bojom 2012.
Ako sjeku x os tada njihove najmanje nultočke pripadaju istom intervalu, a zbog toga će jedna od te dvije nultočke biti najmanja nultočka umnoška te će biti u istom intervalu, a samim time i obojana istom bojom.
![(-{\infty}, 1], (1, 2], (2, 3], ..., (2009, 2010], (2010, +{\infty}]](/media/m/b/b/8/bb874e46630ddef80498ab7ee6a9d61d.png)
Svakom intervalu pridružimo boju (redom slijeva na desno stavljamo boje od 1 do 2011 )
Promotrimo polinom P(x). Imamo 2 slučaja:
1) Ako njegov graf sječe x os onda ga obojamo bojom intervala njegove najmanje nultočke.
2) Ako graf ne sječe x os onda ga obojamo bojom 2012.
Sve boje smo iskoristili.
Neka su polinomi
 i
i 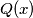 obojani istom bojom.
obojani istom bojom.Ako oni ne sjeku x os tada niti njihov umnožak ne sječe x os pa su sva tri polinoma obojana bojom 2012.
Ako sjeku x os tada njihove najmanje nultočke pripadaju istom intervalu, a zbog toga će jedna od te dvije nultočke biti najmanja nultočka umnoška te će biti u istom intervalu, a samim time i obojana istom bojom.
 Školjka
Školjka  boja (i svaku boju iskoristiti barem jednom) tako da je za svaka dva polinoma iste boje njihov umnožak također te boje?
boja (i svaku boju iskoristiti barem jednom) tako da je za svaka dva polinoma iste boje njihov umnožak također te boje?