Školjka Netočno
25. ožujka 2015. 19:13 (9 godine, 8 mjeseci)
. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka su znamenke broja a1, a2, ..., an. On se može zapisati kao 10 ^ (n - 1) * a1 + 10 ^ (n - 2) * a2 + ... + an = (10 ^ (n - 1) - 1) * a1 + (10 ^ (n - 2) - 1) * a2 + ... + 9 * a(n - 1) + a1 + a2 + ... + an
Svaki broj oblika 10 ^ x - 1 za prirodni broj n je djeljiv s 3, tj. (10 ^ (n - 1) - 1) * a1 + (10 ^ (n - 2) - 1) * a2 + ... + 9 * a(n - 1) je djeljiv s 3, a (10 ^ (n - 1) - 1) * a1 + (10 ^ (n - 2) - 1) * a2 + ... + 9 * a(n - 1) + a1 + a2 + ... + an je djeljiv s 3, pa je (10 ^ (n - 1) - 1) * a1 + (10 ^ (n - 2) - 1) * a2 + ... + 9 * a(n - 1) + a1 + a2 + ... + an - (10 ^ (n - 1) - 1) * a1 + (10 ^ (n - 2) - 1) * a2 + ... + 9 * a(n - 1) = a1 + a2 + ... + an djeljiv s 3.
(znakovi koji su napisani jedan do drugoga ne označavaju množenje nego pojedine znamenke, a operacija množenja je istaknuta
Svaki broj oblika 10 ^ x - 1 za prirodni broj n je djeljiv s 3, tj. (10 ^ (n - 1) - 1) * a1 + (10 ^ (n - 2) - 1) * a2 + ... + 9 * a(n - 1) je djeljiv s 3, a (10 ^ (n - 1) - 1) * a1 + (10 ^ (n - 2) - 1) * a2 + ... + 9 * a(n - 1) + a1 + a2 + ... + an je djeljiv s 3, pa je (10 ^ (n - 1) - 1) * a1 + (10 ^ (n - 2) - 1) * a2 + ... + 9 * a(n - 1) + a1 + a2 + ... + an - (10 ^ (n - 1) - 1) * a1 + (10 ^ (n - 2) - 1) * a2 + ... + 9 * a(n - 1) = a1 + a2 + ... + an djeljiv s 3.
(znakovi koji su napisani jedan do drugoga ne označavaju množenje nego pojedine znamenke, a operacija množenja je istaknuta
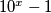djeljiv s