Točno
14. travnja 2012. 21:28 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
a=x^6, b=y^6
množenjem s 12 se dobiva ekvivalentna nejednakost oblika
x^6+y^6+4x^3y^3>=3x^4y^2+3x^2y^4
po A-G vrijedi
(x^6+x^3y^3+x^3y^3)/3>=sqrt 3 (x^12y^6) = x^4y^2
odnosno
(x^6+x^3y^3+x^3y^3)>=3x^4y^2
po A-G vrijedi
(y^6+x^3y^3+x^3y^3)/3>=sqrt 3 (y^12x^6) = y^4x^2
odnosno
(y^6+x^3y^3+x^3y^3)>=3y^4x^2
zbrajajući ove dvije nejednakosti se dobiva polazna nejednakost
množenjem s 12 se dobiva ekvivalentna nejednakost oblika
x^6+y^6+4x^3y^3>=3x^4y^2+3x^2y^4
po A-G vrijedi
(x^6+x^3y^3+x^3y^3)/3>=sqrt 3 (x^12y^6) = x^4y^2
odnosno
(x^6+x^3y^3+x^3y^3)>=3x^4y^2
po A-G vrijedi
(y^6+x^3y^3+x^3y^3)/3>=sqrt 3 (y^12x^6) = y^4x^2
odnosno
(y^6+x^3y^3+x^3y^3)>=3y^4x^2
zbrajajući ove dvije nejednakosti se dobiva polazna nejednakost
 Školjka
Školjka 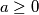 i
i 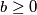 vrijedi nejednakost
vrijedi nejednakost ![\frac{a + \sqrt[3]{a^2b} + \sqrt[3]{ab^2} + b}{4} \leq \frac{a + \sqrt{ab} + b}{3}\text{.}](/media/m/1/c/b/1cb6a951725f0cd08d9806c76d8ff355.png)