Točno
22. svibnja 2012. 13:20 (13 godine, 9 mjeseci)
Ako je
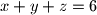
,
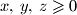
, dokažite da je onda
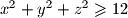
.
%V0
Ako je $x + y + z = 6$, $x,\,y,\,z \geqslant 0$, dokažite da je onda $x^2 + y^2 + z^2 \geqslant 12$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Iz
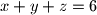
kvadriranjem dobijemo
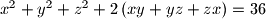
, odnosno
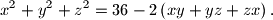
Kako je
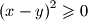
ekvivalentno
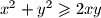
, a analogno vrijedi i
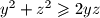
te
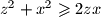
, slijedi
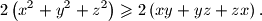
Sada je
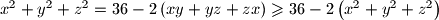
, odakle konačno dobivamo:
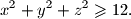
Jednakost vrijedi ako i samo ako je
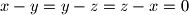
, odnosno
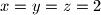
.
%V0
Iz $x + y + z = 6$ kvadriranjem dobijemo $x^2 + y^2 + z^2 + 2 \left(xy + yz + zx\right) = 36$, odnosno $$x^2 + y^2 + z^2 = 36 - 2 \left(xy + yz + zx\right) \text{.}$$
Kako je $\left(x - y\right)^2 \geqslant 0$ ekvivalentno $x^2 + y^2 \geqslant 2xy$, a analogno vrijedi i $y^2 + z^2 \geqslant 2yz$ te $z^2 + x^2 \geqslant 2zx$, slijedi $$2 \left(x^2 + y^2 + z^2\right) \geqslant 2 \left(xy + yz + zx\right) \text{.}$$
Sada je $x^2 + y^2 + z^2 = 36 - 2 \left(xy + yz + zx\right) \geqslant 36 - 2 \left(x^2 + y^2 + z^2\right)$, odakle konačno dobivamo: $$x^2 + y^2 + z^2 \geqslant 12 \text{.}$$
Jednakost vrijedi ako i samo ako je $x - y = y - z = z - x = 0$, odnosno $x = y = z = 2$.
| 22. svibnja 2012. 18:12 | ikicic | Točno |