Točno
23. svibnja 2012. 10:26 (13 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Zadatak smatram izrazito teškim za srednju školu jer nisam uspio naći rješenje koje ne zahtijeva poznavanje diferencijalnog računa.
Pramen pravaca kroz točku određen je jednadžbom
određen je jednadžbom 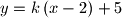 , a sjecišta
, a sjecišta  zadane hiperbole i tih pravaca su rješenja sustava jednadžbi
zadane hiperbole i tih pravaca su rješenja sustava jednadžbi 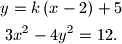
Jasno je da tražimo za koji
za koji 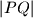 postiže najmanju vrijednost. S obzirom da i
postiže najmanju vrijednost. S obzirom da i 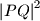 postiže najmanju vrijednost za isti
postiže najmanju vrijednost za isti  dovoljno je promatrati
dovoljno je promatrati 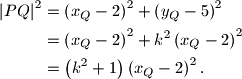
Rješavajući gore navedeni sustav jednadžbi dolazimo do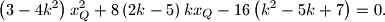
Za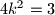 , odnosno
, odnosno 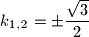 , imamo
, imamo 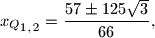 odakle je
odakle je 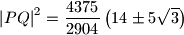 , odnosno
, odnosno 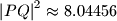 ili
ili 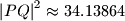 .
.
Za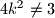 dobijemo
dobijemo 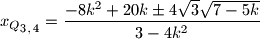 pa je
pa je 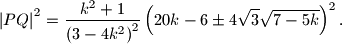
U ovom trenutku možemo odabrati mukotrpno deriviranje složene funkcije ili pomoć nekog alata, npr. Wolfram Alphe.
Ove dvije funkcije postižu minimume (za
(za 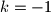 ) i približno
) i približno 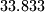 (za
(za 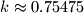 ):
):
1) http://www.wolframalpha.com/input/?i=minimum+%28k%5E2+%2B+1%29+%2F+%283+-+4k%5E2%29%5E2+*+%2820k+-+6+%2B+4Sqrt%5B3%5DSqrt%5B7+-+5k%5D%29%5E2
2) http://www.wolframalpha.com/input/?i=minimum+%28k%5E2+%2B+1%29+%2F+%283+-+4k%5E2%29%5E2+*+%2820k+-+6+-+4Sqrt%5B3%5DSqrt%5B7+-+5k%5D%29%5E2.
Sada je jasno da je točki najbliža točka
najbliža točka 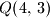 (odgovara slučaju
(odgovara slučaju 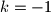 ) i da je njihova udaljenost
) i da je njihova udaljenost 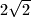 .
.
Pramen pravaca kroz točku
 određen je jednadžbom
određen je jednadžbom 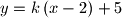 , a sjecišta
, a sjecišta  zadane hiperbole i tih pravaca su rješenja sustava jednadžbi
zadane hiperbole i tih pravaca su rješenja sustava jednadžbi 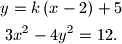
Jasno je da tražimo
 za koji
za koji 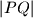 postiže najmanju vrijednost. S obzirom da i
postiže najmanju vrijednost. S obzirom da i 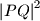 postiže najmanju vrijednost za isti
postiže najmanju vrijednost za isti  dovoljno je promatrati
dovoljno je promatrati 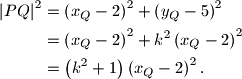
Rješavajući gore navedeni sustav jednadžbi dolazimo do
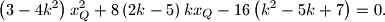
Za
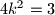 , odnosno
, odnosno 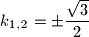 , imamo
, imamo 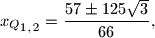 odakle je
odakle je 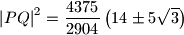 , odnosno
, odnosno 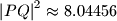 ili
ili 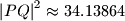 .
.Za
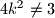 dobijemo
dobijemo 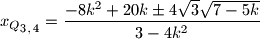 pa je
pa je 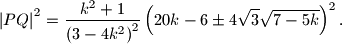
U ovom trenutku možemo odabrati mukotrpno deriviranje složene funkcije ili pomoć nekog alata, npr. Wolfram Alphe.
Ove dvije funkcije postižu minimume
 (za
(za 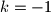 ) i približno
) i približno 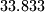 (za
(za 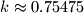 ):
):1) http://www.wolframalpha.com/input/?i=minimum+%28k%5E2+%2B+1%29+%2F+%283+-+4k%5E2%29%5E2+*+%2820k+-+6+%2B+4Sqrt%5B3%5DSqrt%5B7+-+5k%5D%29%5E2
2) http://www.wolframalpha.com/input/?i=minimum+%28k%5E2+%2B+1%29+%2F+%283+-+4k%5E2%29%5E2+*+%2820k+-+6+-+4Sqrt%5B3%5DSqrt%5B7+-+5k%5D%29%5E2.
Sada je jasno da je točki
 najbliža točka
najbliža točka 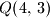 (odgovara slučaju
(odgovara slučaju 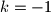 ) i da je njihova udaljenost
) i da je njihova udaljenost 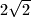 .
. Ocjene: (1)
Komentari:
abulj, 7. kolovoza 2012. 16:13
pbakic, 27. svibnja 2012. 13:53
U svakom slučaju, bez jačih tehnika ne ide? Da su brojevi drukčiji, možda bismo i uspjeli...
Ni meni nije uspjelo nešto lijepo... Probao sam s Lagrangeovim multiplikatorima (točno ovakvi zadaci dođu na kolokvijima na drugoj godini), ali opet ispadne dosta ružan sustav u kojem u najboljem slučaju pogađam rješenja kubne jednadžbe
Zadnja promjena: pbakic, 27. svibnja 2012. 13:54
ikicic, 23. svibnja 2012. 21:47
 Školjka
Školjka 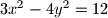 odredi točku najbližu točki
odredi točku najbližu točki 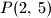 .
. 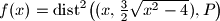 .
.