Točno
26. svibnja 2012. 17:02 (12 godine, 6 mjeseci)
Ako je
,
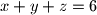
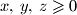
, dokažite da je onda
.
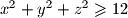
%V0
Ako je $x + y + z = 6$, $x,\,y,\,z \geqslant 0$, dokažite da je onda $x^2 + y^2 + z^2 \geqslant 12$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Iz Cauchyjeve nejednakosti vrijedi:
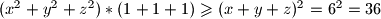
, a iz toga slijedi da je
.
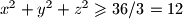
%V0
Iz Cauchyjeve nejednakosti vrijedi:
$(x^2 + y^2 + z^2)*(1 + 1 + 1) \geqslant (x + y + z)^2 = 6^2 = 36$, a iz toga slijedi da je $x^2 + y^2 + z^2 \geqslant 36/3 = 12$.
| 26. svibnja 2012. 20:33 | mljulj | Točno |
| 26. svibnja 2012. 23:15 | ikicic | Točno |
Školjka