Točno
29. svibnja 2012. 16:06 (13 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
jedno zaniljivo rjesenje, koje mi je zapravo matko pokazao:
fiksirajmo sve brojeve osim jednog ( npr, ). tada lijevu stranu mozemo zapisati kao
). tada lijevu stranu mozemo zapisati kao 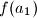 . jasno, to je linearna fucnkcija, odnosno, mozemo ju zapisati kao
. jasno, to je linearna fucnkcija, odnosno, mozemo ju zapisati kao 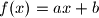 , za neke
, za neke  i
i  . jasno, i minimum i maximum linearne fukcije
. jasno, i minimum i maximum linearne fukcije ![f : R \rightarrow [c, d]](/media/m/1/0/5/10551cb0332c8e55a10fac69b7ddf1eb.png) se postizu u rubovima , tj ili je
se postizu u rubovima , tj ili je 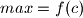 , ili je
, ili je 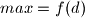 . to mozemo zakljuciti za svaki
. to mozemo zakljuciti za svaki  , dakle ukupni maximum se postize kad je
, dakle ukupni maximum se postize kad je 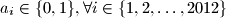 . sad je lako vidjeti da ako je za neki
. sad je lako vidjeti da ako je za neki  ,
, 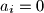 , onda je cijela lijeva strana
, onda je cijela lijeva strana 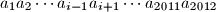 , a to je ocito
, a to je ocito 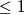 . ako su pak svi
. ako su pak svi 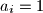 , onda je lijeva strana
, onda je lijeva strana  . dakle, nejednakost je pokazana, a jednakost vrijedi ako i samo ako su svi
. dakle, nejednakost je pokazana, a jednakost vrijedi ako i samo ako su svi  , osim nekog koji je
, osim nekog koji je  .
.
fiksirajmo sve brojeve osim jednog ( npr,
 ). tada lijevu stranu mozemo zapisati kao
). tada lijevu stranu mozemo zapisati kao 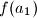 . jasno, to je linearna fucnkcija, odnosno, mozemo ju zapisati kao
. jasno, to je linearna fucnkcija, odnosno, mozemo ju zapisati kao 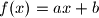 , za neke
, za neke  i
i  . jasno, i minimum i maximum linearne fukcije
. jasno, i minimum i maximum linearne fukcije ![f : R \rightarrow [c, d]](/media/m/1/0/5/10551cb0332c8e55a10fac69b7ddf1eb.png) se postizu u rubovima , tj ili je
se postizu u rubovima , tj ili je 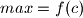 , ili je
, ili je 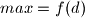 . to mozemo zakljuciti za svaki
. to mozemo zakljuciti za svaki  , dakle ukupni maximum se postize kad je
, dakle ukupni maximum se postize kad je 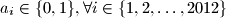 . sad je lako vidjeti da ako je za neki
. sad je lako vidjeti da ako je za neki  ,
, 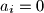 , onda je cijela lijeva strana
, onda je cijela lijeva strana 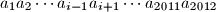 , a to je ocito
, a to je ocito 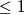 . ako su pak svi
. ako su pak svi 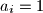 , onda je lijeva strana
, onda je lijeva strana  . dakle, nejednakost je pokazana, a jednakost vrijedi ako i samo ako su svi
. dakle, nejednakost je pokazana, a jednakost vrijedi ako i samo ako su svi  , osim nekog koji je
, osim nekog koji je  .
.  Školjka
Školjka 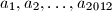 iz intervala
iz intervala ![\left[0,1\right]](/media/m/e/7/f/e7f4d22d3ff05cc9bd2c7aa876c2715c.png) . Dokaži nejednakost:
. Dokaži nejednakost: