Točno
15. travnja 2012. 15:42 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
raspišimo jednakost
2z^3 - 5z^2 - 6iz^2 + 9iz + 1 - 3i = 0
postoji način kako lagano pronaći realno rješenje:
pretpostavimo da je z realan
tada je 6iz^2 + 9iz - 3i = 0
odnosno 2z^2 + 3z - 1 = 0
rješenja su x1=1/2, x2=1
uvrštavajući u jednadžbu, dobiva se da je jedno od rješenja početne jednadžbe z1=1/2
iz osnovnog teorema algebre:
2z^3 - 5z^2 - 6iz^2 + 9iz + 1 - 3i = (z - 1/2) (z - z2) (z - z3)
što znači da (z - 1/2) djeli 2z^3 - 5z^2 - 6iz^2 + 9iz + 1 - 3i
djeljenjem polinoma se dobiva
2z^2 - (4+6i)z - (2-6i) = 0
te se korištenjem kvadratne jednadžbe dobivaju preostala rješenja, z2 = 1+2i, z3 = 1+i
2z^3 - 5z^2 - 6iz^2 + 9iz + 1 - 3i = 0
postoji način kako lagano pronaći realno rješenje:
pretpostavimo da je z realan
tada je 6iz^2 + 9iz - 3i = 0
odnosno 2z^2 + 3z - 1 = 0
rješenja su x1=1/2, x2=1
uvrštavajući u jednadžbu, dobiva se da je jedno od rješenja početne jednadžbe z1=1/2
iz osnovnog teorema algebre:
2z^3 - 5z^2 - 6iz^2 + 9iz + 1 - 3i = (z - 1/2) (z - z2) (z - z3)
što znači da (z - 1/2) djeli 2z^3 - 5z^2 - 6iz^2 + 9iz + 1 - 3i
djeljenjem polinoma se dobiva
2z^2 - (4+6i)z - (2-6i) = 0
te se korištenjem kvadratne jednadžbe dobivaju preostala rješenja, z2 = 1+2i, z3 = 1+i
Ocjene: (1)
Komentari:
kokan, 15. travnja 2012. 18:53
umjesto 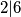 pisite
pisite 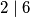 , odnosno
, odnosno 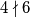
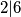 pisite
pisite 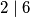 , odnosno
, odnosno 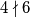
super. cak i jako dobro zapisano :)
evo sam da vidis kako to izgleda malo citljivije, ak stavis dolare na pocetku i kraju mat formula
( iako je u ovom konkretnom slcuaju i ovo sasvim citljivo )
sad, naravno ima par fora tipa da indexe pises ovako:
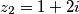 , a razlomke ovako
, a razlomke ovako 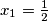 .. i mozes za dijeli napisat ovo
.. i mozes za dijeli napisat ovo 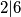 , al dobro, te detalje ces pohvatat s vremenom
, al dobro, te detalje ces pohvatat s vremenom
evo sam da vidis kako to izgleda malo citljivije, ak stavis dolare na pocetku i kraju mat formula
( iako je u ovom konkretnom slcuaju i ovo sasvim citljivo )
raspišimo jednakost
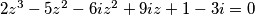
postoji način kako lagano pronaći realno rješenje:
pretpostavimo da je z realan
tada je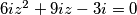
odnosno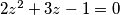
rješenja su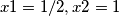
uvrštavajući u jednadžbu, dobiva se da je jedno od rješenja početne jednadžbe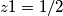
iz osnovnog teorema algebre:
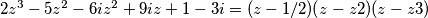
što znači da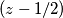 djeli
djeli 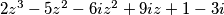
djeljenjem polinoma se dobiva
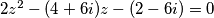
te se korištenjem kvadratne jednadžbe dobivaju preostala rješenja,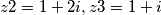
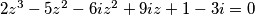
postoji način kako lagano pronaći realno rješenje:
pretpostavimo da je z realan
tada je
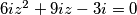
odnosno
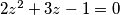
rješenja su
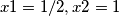
uvrštavajući u jednadžbu, dobiva se da je jedno od rješenja početne jednadžbe
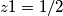
iz osnovnog teorema algebre:
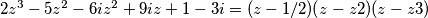
što znači da
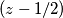 djeli
djeli 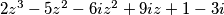
djeljenjem polinoma se dobiva
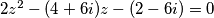
te se korištenjem kvadratne jednadžbe dobivaju preostala rješenja,
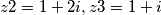
sad, naravno ima par fora tipa da indexe pises ovako:
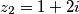 , a razlomke ovako
, a razlomke ovako 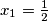 .. i mozes za dijeli napisat ovo
.. i mozes za dijeli napisat ovo 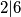 , al dobro, te detalje ces pohvatat s vremenom
, al dobro, te detalje ces pohvatat s vremenomZadnja promjena: kokan, 15. travnja 2012. 18:57
ikicic, 15. travnja 2012. 16:18
grga, 15. travnja 2012. 16:08
super. cak i jako dobro zapisano :)
evo sam da vidis kako to izgleda malo citljivije, ak stavis dolare na pocetku i kraju mat formula
( iako je u ovom konkretnom slcuaju i ovo sasvim citljivo )
sad, naravno ima par fora tipa da indexe pises ovako:
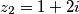 , a razlomke ovako
, a razlomke ovako 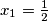 .. i mozes za dijeli napisat ovo
.. i mozes za dijeli napisat ovo 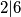 , al dobro, te detalje ces pohvatat s vremenom
, al dobro, te detalje ces pohvatat s vremenom
evo sam da vidis kako to izgleda malo citljivije, ak stavis dolare na pocetku i kraju mat formula
( iako je u ovom konkretnom slcuaju i ovo sasvim citljivo )
raspišimo jednakost
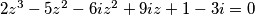
postoji način kako lagano pronaći realno rješenje:
pretpostavimo da je z realan
tada je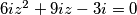
odnosno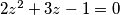
rješenja su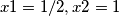
uvrštavajući u jednadžbu, dobiva se da je jedno od rješenja početne jednadžbe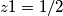
iz osnovnog teorema algebre:
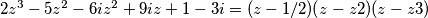
što znači da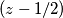 djeli
djeli 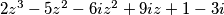
djeljenjem polinoma se dobiva
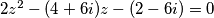
te se korištenjem kvadratne jednadžbe dobivaju preostala rješenja,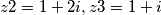
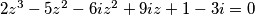
postoji način kako lagano pronaći realno rješenje:
pretpostavimo da je z realan
tada je
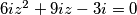
odnosno
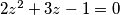
rješenja su
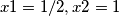
uvrštavajući u jednadžbu, dobiva se da je jedno od rješenja početne jednadžbe
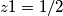
iz osnovnog teorema algebre:
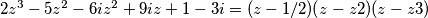
što znači da
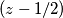 djeli
djeli 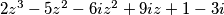
djeljenjem polinoma se dobiva
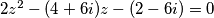
te se korištenjem kvadratne jednadžbe dobivaju preostala rješenja,
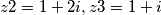
sad, naravno ima par fora tipa da indexe pises ovako:
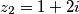 , a razlomke ovako
, a razlomke ovako 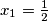 .. i mozes za dijeli napisat ovo
.. i mozes za dijeli napisat ovo 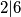 , al dobro, te detalje ces pohvatat s vremenom
, al dobro, te detalje ces pohvatat s vremenom  Školjka
Školjka 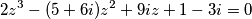 ako se zna da je jedno njezino rješenje realno.
ako se zna da je jedno njezino rješenje realno.