Točno
19. svibnja 2015. 21:57 (10 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
30|n^5-n
30|n(n^4-1)
30|n(n-1)(n+1)(n^2+1)
Da bi broj bio djeljiv s 30, mora biti djeljiv sa 6 i sa 5.
n, n-1, n+1 su tri uzastopna broja, jedan od njih mora biti djeljiv sa dva, a jedan djeljiv sa 3, pa je umnožak djeljiv s 6.
n ≡ 0(mod 5), sve je djeljivo s 5
ako je n ≡ 1(mod 5), n - 1 ≡ 0(mod 5)
ako je n ≡ 4(mod 5), n + 1 ≡ 0(mod 5)
ako je n ≡ 2(mod 5), n^2 + 1 ≡ 0(mod 5)
ako je n ≡ 3(mod 5), n^2 + 1 ≡ 0(mod 5)
30|n(n^4-1)
30|n(n-1)(n+1)(n^2+1)
Da bi broj bio djeljiv s 30, mora biti djeljiv sa 6 i sa 5.
n, n-1, n+1 su tri uzastopna broja, jedan od njih mora biti djeljiv sa dva, a jedan djeljiv sa 3, pa je umnožak djeljiv s 6.
n ≡ 0(mod 5), sve je djeljivo s 5
ako je n ≡ 1(mod 5), n - 1 ≡ 0(mod 5)
ako je n ≡ 4(mod 5), n + 1 ≡ 0(mod 5)
ako je n ≡ 2(mod 5), n^2 + 1 ≡ 0(mod 5)
ako je n ≡ 3(mod 5), n^2 + 1 ≡ 0(mod 5)
 Školjka
Školjka  vrijedi
vrijedi 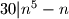 .
.