Točno
25. svibnja 2015. 11:58 (10 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
a^3 = b^2
Prirodni kvadrat mora biti oblika p1^2k * p2^2k ... * pn^2k, a prirodni kub p1^3k * p2^3k ... * pn^3k iz čega slijedi da je a^3 = b^2 = x^6 (potencija prostog faktora lcm(3, 2))
Analogno tome dobivamo da je c^5 = d^4 = y^20
Iz navedenog:
a = x^2
b = x^3
c = y^4
d = y^5
a - c = 9
x^2 - y^4 = 9
(x+y^2)(x-y^2) = 9
9 možemo rastaviti kao 3*3 i 1*9.
Budući da x+y^2 > x-y^2 za svaki x, y > 0, 3 * 3 je nemoguće, a isto tako x-y^2≠9. x^3 > 0 pa x > 0, y^5 > 0 pa y > 0. x^2 > y^4 (jer x^2-y^4=9) pa x > y^2, što isključuje rastavljanje na negativne faktore.
Prema tome:
x-y^2 = 1
x+y^2 = 9
x = 5
y = 2
(a, b, c, d) = (x^2, x^3, y^4, y^5) = (25, 125, 16, 32)
Prirodni kvadrat mora biti oblika p1^2k * p2^2k ... * pn^2k, a prirodni kub p1^3k * p2^3k ... * pn^3k iz čega slijedi da je a^3 = b^2 = x^6 (potencija prostog faktora lcm(3, 2))
Analogno tome dobivamo da je c^5 = d^4 = y^20
Iz navedenog:
a = x^2
b = x^3
c = y^4
d = y^5
a - c = 9
x^2 - y^4 = 9
(x+y^2)(x-y^2) = 9
9 možemo rastaviti kao 3*3 i 1*9.
Budući da x+y^2 > x-y^2 za svaki x, y > 0, 3 * 3 je nemoguće, a isto tako x-y^2≠9. x^3 > 0 pa x > 0, y^5 > 0 pa y > 0. x^2 > y^4 (jer x^2-y^4=9) pa x > y^2, što isključuje rastavljanje na negativne faktore.
Prema tome:
x-y^2 = 1
x+y^2 = 9
x = 5
y = 2
(a, b, c, d) = (x^2, x^3, y^4, y^5) = (25, 125, 16, 32)
 Školjka
Školjka 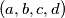 prirodnih brojeva takve da je
prirodnih brojeva takve da je 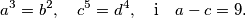
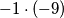 i slicno. Naravno, odgovor je jer se radi o prirodnim (pozitivnim) brojevima. Takodjer, opcenito moze biti razlicito
i slicno. Naravno, odgovor je jer se radi o prirodnim (pozitivnim) brojevima. Takodjer, opcenito moze biti razlicito 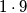 i
i 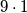 .
.