Točno
25. svibnja 2015. 21:02 (10 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ako je p neparan prost broj, p^q + 1 je paran broj te nije prost. Prema tome, p = 2
S obzirom na kongruentnost modulo 3, potencije broja 2 pokazuju sljedeće:
2^0 ≡ 1 (mod 3)
2^1 ≡ 2 (mod 3)
2^2 ≡ 1 (mod 3)
ili:
2^2k ≡ 1(mod 3)
2^(2k-1) ≡ 2(mod 3)
Prema tome, 2^(2k-1) + 1 ≡ 0(mod 3) te nije prost, pa q može biti samo paran broj.
Jedino rješenje je (p, q) = (2, 2)
S obzirom na kongruentnost modulo 3, potencije broja 2 pokazuju sljedeće:
2^0 ≡ 1 (mod 3)
2^1 ≡ 2 (mod 3)
2^2 ≡ 1 (mod 3)
ili:
2^2k ≡ 1(mod 3)
2^(2k-1) ≡ 2(mod 3)
Prema tome, 2^(2k-1) + 1 ≡ 0(mod 3) te nije prost, pa q može biti samo paran broj.
Jedino rješenje je (p, q) = (2, 2)
 Školjka
Školjka  i
i  takve da je
takve da je 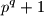 također prost.
također prost.