Točno
28. svibnja 2015. 14:18 (10 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
a^4-10a^2+9 = a^4-9a^2-a^2+9 = (a^2-1)(a^2-9) = (a+1)(a-1)(a-3)(a+3)
1920 = (2^7)*3*5
a > 5, a je prost
a ≡ 1(mod 3), a-1 ≡ 0(mod 3)
a ≡ 2(mod 3), a+1 ≡ 0(mod 3)
Izraz je djeljiv sa 3.
a ≡ 1(mod 5), a-1 ≡ 0(mod 5)
a ≡ 2(mod 5), a+3 ≡ 0(mod 5)
a ≡ 3(mod 5), a-3 ≡ 0(mod 5)
a ≡ 4(mod 5), a+1 ≡ 0(mod 5)
Izraz je djeljiv sa 5.
a ≡ 1(mod 2)
Svi elementi rastavljenog izraza (a+3. a-1, a+1, a-3) su djeljivi sa 2.
Izraz je djeljiv sa 16.
a ≡ 1(mod 4)
a-1, a+3 ≡ 0(mod 4)
a ≡ 3(mod 4)
a+1, a-3 ≡ 0(mod 4)
a ≡ 2(mod 4) -> broj nije prost
Izraz je uvijek još dvaput djeljiv sa 2.
Izraz je djeljiv sa 64.
a ≡ 1(mod 8), a-1 ≡ 0(mod 8)
a ≡ 3(mod 8), a-3 ≡ 0(mod 8)
a ≡ 5(mod 8), a+3 ≡ 0(mod 8)
a ≡ 7(mod 8), a+1 ≡ 0(mod 8)
ako je a ≡ 2k(mod 8), a nije prost
Izraz je uvijek još jednom djeljiv sa 2.
Izraz je djeljiv sa 128 (2^7)
Ako je izraz djeljiv sa 128, 3 i 5, djeljiv je sa 1920.
1920 = (2^7)*3*5
a > 5, a je prost
a ≡ 1(mod 3), a-1 ≡ 0(mod 3)
a ≡ 2(mod 3), a+1 ≡ 0(mod 3)
Izraz je djeljiv sa 3.
a ≡ 1(mod 5), a-1 ≡ 0(mod 5)
a ≡ 2(mod 5), a+3 ≡ 0(mod 5)
a ≡ 3(mod 5), a-3 ≡ 0(mod 5)
a ≡ 4(mod 5), a+1 ≡ 0(mod 5)
Izraz je djeljiv sa 5.
a ≡ 1(mod 2)
Svi elementi rastavljenog izraza (a+3. a-1, a+1, a-3) su djeljivi sa 2.
Izraz je djeljiv sa 16.
a ≡ 1(mod 4)
a-1, a+3 ≡ 0(mod 4)
a ≡ 3(mod 4)
a+1, a-3 ≡ 0(mod 4)
a ≡ 2(mod 4) -> broj nije prost
Izraz je uvijek još dvaput djeljiv sa 2.
Izraz je djeljiv sa 64.
a ≡ 1(mod 8), a-1 ≡ 0(mod 8)
a ≡ 3(mod 8), a-3 ≡ 0(mod 8)
a ≡ 5(mod 8), a+3 ≡ 0(mod 8)
a ≡ 7(mod 8), a+1 ≡ 0(mod 8)
ako je a ≡ 2k(mod 8), a nije prost
Izraz je uvijek još jednom djeljiv sa 2.
Izraz je djeljiv sa 128 (2^7)
Ako je izraz djeljiv sa 128, 3 i 5, djeljiv je sa 1920.
 Školjka
Školjka 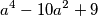 djeljiv s
djeljiv s 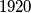 za svaki prosti broj
za svaki prosti broj 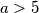 .
.