Točno
27. svibnja 2015. 12:57 (10 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
6^m + 2^n +2 = x^2
x mora biti paran broj, a ako je x paran, x^2 ≡ 0(mod 4)
Suma 6^m + 2^n je djeljiva sa 4 za svaki m, n > 1, pa izraz 6^m+2^n+2 nije djeljiv sa 4.
Prema tome, m ili n mora biti jednako 1.
a) m = 1
6 + 2^n +2 = x^2
2^n + 8 = x^2
Za svaki n > 3, 2^n ≡ 0(mod 16) pa 2^n+8 ≡ 8(mod 16)
Potpun kvadrat ne može biti djeljiv samo sa 8, a ne sa 16(jer u prostoj faktorizaciji broja može biti 1, 2, 3, 4.. broja 2 a u fakt. njegova kvadrata 2, 4, 6, 8 njih), pa n ne može biti veće od 3.
2^1 + 8 = 10 (nije potpun)
2^2 + 8 = 12 (nije potpun)
2^3 + 8 = 16 (potpun kvadrat)
b) n = 1
6^m + 2 + 2 = x^2
6^m + 4 = x^2
6^m ≡ 1(mod 7) za parne m, pa 6^m + 4 ≡ 5(mod 7)
6^m ≡ 6(mod 7) za neparne n, pa 6^m + 4 ≡ 3(mod 7)
Analizom ostataka potpunih kvadrata pri dijeljenju sa 7 uviđamo da su kongruentni 0, 1, 4, 2, 2, 4, 1 mod 7, pa 6^m + 4 nikako ne može biti potpun kvadrat.
Jedino rješenje je (m, n) = (1, 3).
x mora biti paran broj, a ako je x paran, x^2 ≡ 0(mod 4)
Suma 6^m + 2^n je djeljiva sa 4 za svaki m, n > 1, pa izraz 6^m+2^n+2 nije djeljiv sa 4.
Prema tome, m ili n mora biti jednako 1.
a) m = 1
6 + 2^n +2 = x^2
2^n + 8 = x^2
Za svaki n > 3, 2^n ≡ 0(mod 16) pa 2^n+8 ≡ 8(mod 16)
Potpun kvadrat ne može biti djeljiv samo sa 8, a ne sa 16(jer u prostoj faktorizaciji broja može biti 1, 2, 3, 4.. broja 2 a u fakt. njegova kvadrata 2, 4, 6, 8 njih), pa n ne može biti veće od 3.
2^1 + 8 = 10 (nije potpun)
2^2 + 8 = 12 (nije potpun)
2^3 + 8 = 16 (potpun kvadrat)
b) n = 1
6^m + 2 + 2 = x^2
6^m + 4 = x^2
6^m ≡ 1(mod 7) za parne m, pa 6^m + 4 ≡ 5(mod 7)
6^m ≡ 6(mod 7) za neparne n, pa 6^m + 4 ≡ 3(mod 7)
Analizom ostataka potpunih kvadrata pri dijeljenju sa 7 uviđamo da su kongruentni 0, 1, 4, 2, 2, 4, 1 mod 7, pa 6^m + 4 nikako ne može biti potpun kvadrat.
Jedino rješenje je (m, n) = (1, 3).
 Školjka
Školjka  i
i  za koje je
za koje je 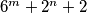 potpun kvadrat.
potpun kvadrat.