Točno
27. svibnja 2015. 17:45 (9 godine, 6 mjeseci)
Pokažite da za svaka dva pozitivna broja
i
vrijedi nejednakost
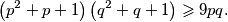
%V0
Pokažite da za svaka dva pozitivna broja $p$ i $q$ vrijedi nejednakost $$\left(p^2+p+1\right)\left(q^2+q+1\right) \geqslant 9pq \text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Rastavimo nejednadžbu ovako:
p^2 + p + 1 ≥ 3p
p^2 - 2p + 1 ≥ 0
(p - 1)^2 ≥ 0
što vrijedi za svaki realan broj p
q^2 + q + 1 ≥ 3q
q^2 - 2q + 1 ≥ 0
(q - 1)^2 ≥ 0
što vrijedi za svaki realan broj q
Pomnoživši dokazane nejednakosti dobivamo originalnu nejednakost, što ju dokazuje.
%V0
Rastavimo nejednadžbu ovako:
p^2 + p + 1 ≥ 3p
p^2 - 2p + 1 ≥ 0
(p - 1)^2 ≥ 0
što vrijedi za svaki realan broj p
q^2 + q + 1 ≥ 3q
q^2 - 2q + 1 ≥ 0
(q - 1)^2 ≥ 0
što vrijedi za svaki realan broj q
Pomnoživši dokazane nejednakosti dobivamo originalnu nejednakost, što ju dokazuje.
| 27. svibnja 2015. 22:04 | ikicic | Točno |
Školjka