Točno
29. svibnja 2015. 20:38 (10 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Vidimo da stranica AQ je ujedno i stranica trokuta  DAQ
DAQ
Trokut DAQ je jednakokračan jer su mu stranice DA i QD jednake duljine što proizlazi iz toga da su stranice jednakostraničnih trokutova
DAQ je jednakokračan jer su mu stranice DA i QD jednake duljine što proizlazi iz toga da su stranice jednakostraničnih trokutova  BPC i
BPC i  DCQ jednake stranicama kvadrata jer su jednakostranični trokutovi konstruirani nad stranicama kvadrata a stranica kvadrata je jedna od svih jednakih stranica tih trokutova.
DCQ jednake stranicama kvadrata jer su jednakostranični trokutovi konstruirani nad stranicama kvadrata a stranica kvadrata je jedna od svih jednakih stranica tih trokutova.
Kutovi nasuprot jednakih stranica jednakokračnog trokuta su jednaki.
Kut nasuprot stranice AQ je zbroj veličina kutova CDA i
CDA i  QDC .Kako su kutovi jednakostraničnih trokutova
QDC .Kako su kutovi jednakostraničnih trokutova 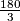 =60°,zaključujemo da je i kut
=60°,zaključujemo da je i kut  QDC veličine 60°,a kutovi kvadrata su
QDC veličine 60°,a kutovi kvadrata su =90°,pa je tako kut
=90°,pa je tako kut  ADC također veličine 90°.To bi značilo da je kut nasuprot stranice AQ jednak 90°+60°=150° a svaki od kutova
ADC također veličine 90°.To bi značilo da je kut nasuprot stranice AQ jednak 90°+60°=150° a svaki od kutova  DAQ i
DAQ i  AQD imaju veličinu
AQD imaju veličinu 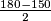 =
=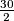 =15°
=15°
Trokut ABP je jednak trokutu
ABP je jednak trokutu  DAQ zbog duljina stranica AB i BP.
DAQ zbog duljina stranica AB i BP.
Kut DAB kao kut kvadrata ima 90°,a kako je kut
DAB kao kut kvadrata ima 90°,a kako je kut  DAB=
DAB=  DAQ+
DAQ+  QAP+
QAP+ PAB vrijedi
PAB vrijedi
90°=2*15°+ QAP
QAP
90°=30°+ QAP
QAP
 QAP=90°-30°
QAP=90°-30°
 QAP=60°
QAP=60°
Kut QAP je jedan od kutova trokuta
QAP je jedan od kutova trokuta  APQ stoga je zbroj kutova
APQ stoga je zbroj kutova  PQA i
PQA i  APQ=180°-60°=120°
APQ=180°-60°=120°
Kako bismo izračunali duljinu stranice PQ možemo se koristiti trokutom CPQ koji je jednak trokutovima
CPQ koji je jednak trokutovima  ABP i DAQ zbog duljina stranica QC i CP.Kako su one jednake a i kutovi(to možemo izračunati jer je veličina kuta
ABP i DAQ zbog duljina stranica QC i CP.Kako su one jednake a i kutovi(to možemo izračunati jer je veličina kuta  CPQ=360°-(90°+60°*2)=360°-(90°+120°)=360°-210°=150°,a to je jednako kao i veličina kuta
CPQ=360°-(90°+60°*2)=360°-(90°+120°)=360°-210°=150°,a to je jednako kao i veličina kuta  QAD) to znači da je i stranica PQ jednake duljine duljinama stranica QA i AP iz čega zaključujem da je trokut
QAD) to znači da je i stranica PQ jednake duljine duljinama stranica QA i AP iz čega zaključujem da je trokut  APQ jednakostraničan što potvrđuje i veličina kuta
APQ jednakostraničan što potvrđuje i veličina kuta  QAP koja je 60°,a kako sam još prije utvrdila da su stranice QA i AP jednake duljine,bilo je moguće i izračunati kutove
QAP koja je 60°,a kako sam još prije utvrdila da su stranice QA i AP jednake duljine,bilo je moguće i izračunati kutove  PQA i
PQA i  APQ kao i kutove bilo kojeg jednakokračnog(a jednakostraničan je kao ''vrha'' jednakokračnog)trokuta
APQ kao i kutove bilo kojeg jednakokračnog(a jednakostraničan je kao ''vrha'' jednakokračnog)trokuta  PQA=
PQA=  APQ=
APQ=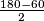 =
=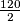 =60°
=60°
 DAQ
DAQTrokut
 DAQ je jednakokračan jer su mu stranice DA i QD jednake duljine što proizlazi iz toga da su stranice jednakostraničnih trokutova
DAQ je jednakokračan jer su mu stranice DA i QD jednake duljine što proizlazi iz toga da su stranice jednakostraničnih trokutova  BPC i
BPC i  DCQ jednake stranicama kvadrata jer su jednakostranični trokutovi konstruirani nad stranicama kvadrata a stranica kvadrata je jedna od svih jednakih stranica tih trokutova.
DCQ jednake stranicama kvadrata jer su jednakostranični trokutovi konstruirani nad stranicama kvadrata a stranica kvadrata je jedna od svih jednakih stranica tih trokutova.Kutovi nasuprot jednakih stranica jednakokračnog trokuta su jednaki.
Kut nasuprot stranice AQ je zbroj veličina kutova
 CDA i
CDA i  QDC .Kako su kutovi jednakostraničnih trokutova
QDC .Kako su kutovi jednakostraničnih trokutova 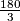 =60°,zaključujemo da je i kut
=60°,zaključujemo da je i kut  QDC veličine 60°,a kutovi kvadrata su
QDC veličine 60°,a kutovi kvadrata su =90°,pa je tako kut
=90°,pa je tako kut  ADC također veličine 90°.To bi značilo da je kut nasuprot stranice AQ jednak 90°+60°=150° a svaki od kutova
ADC također veličine 90°.To bi značilo da je kut nasuprot stranice AQ jednak 90°+60°=150° a svaki od kutova  DAQ i
DAQ i  AQD imaju veličinu
AQD imaju veličinu 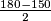 =
=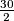 =15°
=15°Trokut
 ABP je jednak trokutu
ABP je jednak trokutu  DAQ zbog duljina stranica AB i BP.
DAQ zbog duljina stranica AB i BP.Kut
 DAB kao kut kvadrata ima 90°,a kako je kut
DAB kao kut kvadrata ima 90°,a kako je kut  DAB=
DAB=  DAQ+
DAQ+  QAP+
QAP+ PAB vrijedi
PAB vrijedi 90°=2*15°+
 QAP
QAP90°=30°+
 QAP
QAP QAP=90°-30°
QAP=90°-30° QAP=60°
QAP=60° Kut
 QAP je jedan od kutova trokuta
QAP je jedan od kutova trokuta  APQ stoga je zbroj kutova
APQ stoga je zbroj kutova  PQA i
PQA i  APQ=180°-60°=120°
APQ=180°-60°=120°Kako bismo izračunali duljinu stranice PQ možemo se koristiti trokutom
 CPQ koji je jednak trokutovima
CPQ koji je jednak trokutovima  ABP i DAQ zbog duljina stranica QC i CP.Kako su one jednake a i kutovi(to možemo izračunati jer je veličina kuta
ABP i DAQ zbog duljina stranica QC i CP.Kako su one jednake a i kutovi(to možemo izračunati jer je veličina kuta  CPQ=360°-(90°+60°*2)=360°-(90°+120°)=360°-210°=150°,a to je jednako kao i veličina kuta
CPQ=360°-(90°+60°*2)=360°-(90°+120°)=360°-210°=150°,a to je jednako kao i veličina kuta  QAD) to znači da je i stranica PQ jednake duljine duljinama stranica QA i AP iz čega zaključujem da je trokut
QAD) to znači da je i stranica PQ jednake duljine duljinama stranica QA i AP iz čega zaključujem da je trokut  APQ jednakostraničan što potvrđuje i veličina kuta
APQ jednakostraničan što potvrđuje i veličina kuta  QAP koja je 60°,a kako sam još prije utvrdila da su stranice QA i AP jednake duljine,bilo je moguće i izračunati kutove
QAP koja je 60°,a kako sam još prije utvrdila da su stranice QA i AP jednake duljine,bilo je moguće i izračunati kutove  PQA i
PQA i  APQ kao i kutove bilo kojeg jednakokračnog(a jednakostraničan je kao ''vrha'' jednakokračnog)trokuta
APQ kao i kutove bilo kojeg jednakokračnog(a jednakostraničan je kao ''vrha'' jednakokračnog)trokuta  PQA=
PQA=  APQ=
APQ=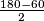 =
=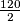 =60°
=60° Ocjene: (1)
Komentari:
PatricijaVelecki, 30. svibnja 2015. 14:02
Aha,a to je zato što sam poznata po tom da kompliciram i najjednostavnije stvari(jer uvijek pokušam sve na onoliko načina koliko se mogu sjetiti i to posebno nakon ovogodišnjeg županijskog natjecanja) :)
Nije greška. Samo kažem da si mogla puno prije dovrišiti dokaz.
Taman dokažeš sve što ti treba, a onda skreneš i napraviš sve ponovno na drugi način :P
Taman dokažeš sve što ti treba, a onda skreneš i napraviš sve ponovno na drugi način :P
Hvala na komentaru,ali nije mi baš potpuno jasno kako su to dva različita dokaza?
Sad me to zanima jer se bojim da ću u nekom drugom zadatku napraviti veću grešku ili pak istu
Sad me to zanima jer se bojim da ću u nekom drugom zadatku napraviti veću grešku ili pak istu
Zadnja promjena: PatricijaVelecki, 30. svibnja 2015. 14:02
ikicic, 30. svibnja 2015. 13:44
Nije greška. Samo kažem da si mogla puno prije dovrišiti dokaz.
Taman dokažeš sve što ti treba, a onda skreneš i napraviš sve ponovno na drugi način :P
Taman dokažeš sve što ti treba, a onda skreneš i napraviš sve ponovno na drugi način :P
Hvala na komentaru,ali nije mi baš potpuno jasno kako su to dva različita dokaza?
Sad me to zanima jer se bojim da ću u nekom drugom zadatku napraviti veću grešku ili pak istu
Sad me to zanima jer se bojim da ću u nekom drugom zadatku napraviti veću grešku ili pak istu
PatricijaVelecki, 30. svibnja 2015. 11:14
Hvala na komentaru,ali nije mi baš potpuno jasno kako su to dva različita dokaza?
Sad me to zanima jer se bojim da ću u nekom drugom zadatku napraviti veću grešku ili pak istu
Sad me to zanima jer se bojim da ću u nekom drugom zadatku napraviti veću grešku ili pak istu
Točno je. (ne ispravljam geometriju inače jer osim jednostavnijih stvari ju ne znam baš)
Kratki komentar. Ti si ovdje navela praktički dva različita dokaza.
Na kraju prvog paragrafa kažeš da je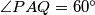 , što uz
, što uz 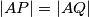 automatski znači da je trokut
automatski znači da je trokut 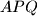 jednakostraničan.
jednakostraničan.
U drugom paragrafu pak praktički pokažeš da su trokuti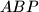 ,
, 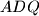 i
i 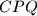 sukladni, što opet znači da je trokut
sukladni, što opet znači da je trokut 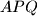 jednakostraničan.
jednakostraničan.
Kratki komentar. Ti si ovdje navela praktički dva različita dokaza.
Na kraju prvog paragrafa kažeš da je
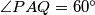 , što uz
, što uz 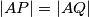 automatski znači da je trokut
automatski znači da je trokut 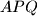 jednakostraničan.
jednakostraničan.U drugom paragrafu pak praktički pokažeš da su trokuti
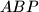 ,
, 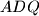 i
i 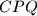 sukladni, što opet znači da je trokut
sukladni, što opet znači da je trokut 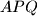 jednakostraničan.
jednakostraničan.ikicic, 30. svibnja 2015. 10:50
Točno je. (ne ispravljam geometriju inače jer osim jednostavnijih stvari ju ne znam baš)
Kratki komentar. Ti si ovdje navela praktički dva različita dokaza.
Na kraju prvog paragrafa kažeš da je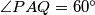 , što uz
, što uz 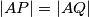 automatski znači da je trokut
automatski znači da je trokut 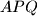 jednakostraničan.
jednakostraničan.
U drugom paragrafu pak praktički pokažeš da su trokuti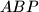 ,
, 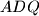 i
i 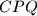 sukladni, što opet znači da je trokut
sukladni, što opet znači da je trokut 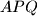 jednakostraničan.
jednakostraničan.
Kratki komentar. Ti si ovdje navela praktički dva različita dokaza.
Na kraju prvog paragrafa kažeš da je
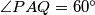 , što uz
, što uz 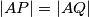 automatski znači da je trokut
automatski znači da je trokut 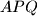 jednakostraničan.
jednakostraničan.U drugom paragrafu pak praktički pokažeš da su trokuti
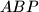 ,
, 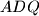 i
i 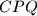 sukladni, što opet znači da je trokut
sukladni, što opet znači da je trokut 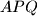 jednakostraničan.
jednakostraničan. Zadnja promjena: ikicic, 30. svibnja 2015. 10:50
PatricijaVelecki, 30. svibnja 2015. 07:08
PatricijaVelecki, 30. svibnja 2015. 06:58
 Školjka
Školjka  i
i  kvadrata
kvadrata  konstruirani su jednakostranični trokuti
konstruirani su jednakostranični trokuti 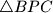 i
i 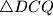 . Dokažite da je trokut
. Dokažite da je trokut 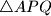 jednakostraničan.
jednakostraničan. 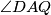 umjesto
umjesto