Točno
30. svibnja 2015. 22:33 (10 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Označimo sa 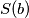 sumu bitka svih sudionika kampa. Pri početku kampa nitko nikoga ne poznaje pa je
sumu bitka svih sudionika kampa. Pri početku kampa nitko nikoga ne poznaje pa je 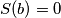 . Pri svakom upoznavanju dviju osoba, bitak osoba koje se upoznaju se povećava za
. Pri svakom upoznavanju dviju osoba, bitak osoba koje se upoznaju se povećava za  , pa se
, pa se 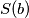 povećava za
povećava za  . Nizom takvih upoznavanja se nikada ne dolazi do neparnoga broja. Naravno, sve ovo podrazumijeva da je nemoguće poznavati neku osobu bez da ona poznaje vas, a budući da na matematičkom kampu sudjeluju samo
. Nizom takvih upoznavanja se nikada ne dolazi do neparnoga broja. Naravno, sve ovo podrazumijeva da je nemoguće poznavati neku osobu bez da ona poznaje vas, a budući da na matematičkom kampu sudjeluju samo 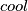 ljudi, a ne stalkeri, možemo isključiti taj slučaj.
ljudi, a ne stalkeri, možemo isključiti taj slučaj.
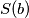 sumu bitka svih sudionika kampa. Pri početku kampa nitko nikoga ne poznaje pa je
sumu bitka svih sudionika kampa. Pri početku kampa nitko nikoga ne poznaje pa je 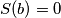 . Pri svakom upoznavanju dviju osoba, bitak osoba koje se upoznaju se povećava za
. Pri svakom upoznavanju dviju osoba, bitak osoba koje se upoznaju se povećava za  , pa se
, pa se 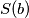 povećava za
povećava za  . Nizom takvih upoznavanja se nikada ne dolazi do neparnoga broja. Naravno, sve ovo podrazumijeva da je nemoguće poznavati neku osobu bez da ona poznaje vas, a budući da na matematičkom kampu sudjeluju samo
. Nizom takvih upoznavanja se nikada ne dolazi do neparnoga broja. Naravno, sve ovo podrazumijeva da je nemoguće poznavati neku osobu bez da ona poznaje vas, a budući da na matematičkom kampu sudjeluju samo 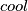 ljudi, a ne stalkeri, možemo isključiti taj slučaj.
ljudi, a ne stalkeri, možemo isključiti taj slučaj. Ocjene: (1)
Komentari:
ikicic, 30. svibnja 2015. 21:51
Na EMCu ove godine sam zažalio što nisam točno rekao koliko nečega će biti u ovisnosti o početno n, pa imam naviku odrediti sve moguće, makar nepotrebno.
Treba prakse da se nauci dobro pisati rjesenja, zato je dobro sto se organiziraju dodatna natjecanja pored drzavnih i olimpijada.
Ako rjesenje ima nekih sumnjivih koraka, pitanje je li tocno uopce. Zato se forsira formalnost. A i koliko je jasno napisano rjesenje govori o tome koliko je tebi samome jasno xD
Recimo ovdje se dobije dojam da mislis da se opceniti slucaj poznanstava svodi na potpun graf, sto je krivo.
Kad bi izbacio to u zagradi i ono s maksimalnim brojem rjesenje bi bilo sasvim u redu.
matsimic, 30. svibnja 2015. 20:32
Trebalo je to malo elegantnije reći - maksimalno toliko, ali uvijek na upoznavanja dviju ljudi. Planiram provjeriti pretpostavku ove godine pa ću moći sa sigurnošću reći. Na EMCu ove godine sam zažalio što nisam točno rekao koliko nečega će biti u ovisnosti o početno n, pa imam naviku odrediti sve moguće, makar nepotrebno.
ikicic, 30. svibnja 2015. 20:20
Haha, slobodno mozes pretpostaviti da su na kampu samo 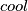 ljudi.
ljudi.
Ne mora uvijek graf poznanstava biti potpun (da svatko od tih poznaje svih ostalih
poznaje svih ostalih  ). Moguci su i drugaciji slucajevi. Npr. A i B se poznaju, B i C se poznaju, ali ne i A i C.
). Moguci su i drugaciji slucajevi. Npr. A i B se poznaju, B i C se poznaju, ali ne i A i C.
Takodjer, zasto je bitno koliki je maksimalni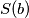 ? xD
? xD
(Nije problem, samo pokusavam sto vise skratiti rjesenja)
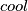 ljudi.
ljudi.(a svako upoznavanje  ljudi se može rastaviti na
ljudi se može rastaviti na 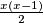 upoznavanja dviju osoba)
upoznavanja dviju osoba)
 ljudi se može rastaviti na
ljudi se može rastaviti na 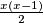 upoznavanja dviju osoba)
upoznavanja dviju osoba)Ne mora uvijek graf poznanstava biti potpun (da svatko od tih
 poznaje svih ostalih
poznaje svih ostalih  ). Moguci su i drugaciji slucajevi. Npr. A i B se poznaju, B i C se poznaju, ali ne i A i C.
). Moguci su i drugaciji slucajevi. Npr. A i B se poznaju, B i C se poznaju, ali ne i A i C.Takodjer, zasto je bitno koliki je maksimalni
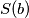 ? xD
? xD(Nije problem, samo pokusavam sto vise skratiti rjesenja)
 Školjka
Školjka  ljudi. Na početku kampa nitko nikoga ne poznaje. Nazovimo bitak neke osobe broj ljudi koje ta osoba poznaje. Dokaži da je suma bitaka svih sudionika kampa parna.
ljudi. Na početku kampa nitko nikoga ne poznaje. Nazovimo bitak neke osobe broj ljudi koje ta osoba poznaje. Dokaži da je suma bitaka svih sudionika kampa parna.