Točno
4. lipnja 2015. 13:43 (10 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Niz sadržava sve brojeve oblika 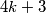 veće od
veće od 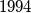 , pa da bi sadržavao beskonačno mnogo prostih brojeva mora biti beskonačno mnogo prostih brojeva oblika
, pa da bi sadržavao beskonačno mnogo prostih brojeva mora biti beskonačno mnogo prostih brojeva oblika 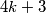 .
.
Pretpostavimo suprotno: postoji konačan broj prostih brojeva oblika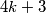 . Označimo njihov umnožak
. Označimo njihov umnožak 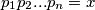 .
.
Promatrajmo dva slučaja:
I. broj prostih brojeva oblika
prostih brojeva oblika 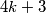 je paran
je paran
U tom slučaju je oblika
oblika 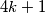 .
. 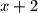 je kongruentan
je kongruentan  i nije djeljiv niti s jednim od brojeva
i nije djeljiv niti s jednim od brojeva 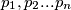 . Da bi broj bio oblika
. Da bi broj bio oblika 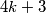 , neparan broj njegovih prostih faktora mora biti oblika
, neparan broj njegovih prostih faktora mora biti oblika 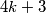 a budući da nije djeljiv niti s jednim brojem s "popisa" mora postojati još neki prosti broj oblika
a budući da nije djeljiv niti s jednim brojem s "popisa" mora postojati još neki prosti broj oblika 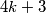 što vodi do kontradikcije u slučaju I.
što vodi do kontradikcije u slučaju I.
II. broj prostih brojeva
prostih brojeva 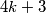 je neparan
je neparan
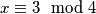 pa promatramo
pa promatramo 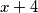 .
.
On nije djeljiv niti s jednim od brojeva sa "popisa" što vodi do kontradikcije i u slučaju II.
Prema tome, mora postojati beskonačan broj prostih brojeva oblika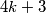 i zadani niz će sadržavati sve veće od
i zadani niz će sadržavati sve veće od 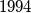 .
.
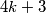 veće od
veće od 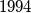 , pa da bi sadržavao beskonačno mnogo prostih brojeva mora biti beskonačno mnogo prostih brojeva oblika
, pa da bi sadržavao beskonačno mnogo prostih brojeva mora biti beskonačno mnogo prostih brojeva oblika 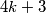 .
.Pretpostavimo suprotno: postoji konačan broj prostih brojeva oblika
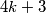 . Označimo njihov umnožak
. Označimo njihov umnožak 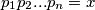 .
.Promatrajmo dva slučaja:
I. broj
 prostih brojeva oblika
prostih brojeva oblika 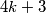 je paran
je paranU tom slučaju je
 oblika
oblika 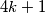 .
. 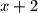 je kongruentan
je kongruentan  i nije djeljiv niti s jednim od brojeva
i nije djeljiv niti s jednim od brojeva 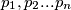 . Da bi broj bio oblika
. Da bi broj bio oblika 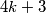 , neparan broj njegovih prostih faktora mora biti oblika
, neparan broj njegovih prostih faktora mora biti oblika 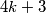 a budući da nije djeljiv niti s jednim brojem s "popisa" mora postojati još neki prosti broj oblika
a budući da nije djeljiv niti s jednim brojem s "popisa" mora postojati još neki prosti broj oblika 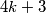 što vodi do kontradikcije u slučaju I.
što vodi do kontradikcije u slučaju I.II. broj
 prostih brojeva
prostih brojeva 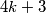 je neparan
je neparan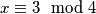 pa promatramo
pa promatramo 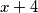 .
.On nije djeljiv niti s jednim od brojeva sa "popisa" što vodi do kontradikcije i u slučaju II.
Prema tome, mora postojati beskonačan broj prostih brojeva oblika
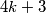 i zadani niz će sadržavati sve veće od
i zadani niz će sadržavati sve veće od 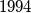 .
. Ocjene: (1)
Komentari:
matsimic, 7. lipnja 2015. 22:58
ikicic, 7. lipnja 2015. 22:14
Zanimljiv naziv xD Cak me i ne cudi, ti svi problemi su vrlo jednostavni za izreci i moze ih bilo tko sjetiti, ali su izgleda brutalno teski za dokazati :)
Isto vrijedi i za manje poznate vrste kao sexy primes i Wagstaff primes te za bilo koji prime gap  gdje je
gdje je 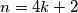 po Polignacu. Zanimljivo kako je srednjoškolski zadatak povezan s većim problemima moderne matematike.
po Polignacu. Zanimljivo kako je srednjoškolski zadatak povezan s većim problemima moderne matematike.
 gdje je
gdje je 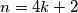 po Polignacu. Zanimljivo kako je srednjoškolski zadatak povezan s većim problemima moderne matematike.
po Polignacu. Zanimljivo kako je srednjoškolski zadatak povezan s većim problemima moderne matematike.ikicic, 4. lipnja 2015. 20:35
ikicic, 4. lipnja 2015. 20:17
matsimic, 4. lipnja 2015. 20:01
ikicic, 4. lipnja 2015. 14:51
matsimic, 4. lipnja 2015. 13:42
ikicic, 4. lipnja 2015. 11:18
 Školjka
Školjka 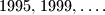 Dokažite da taj niz sadrži beskonačno mnogo prostih brojeva.
Dokažite da taj niz sadrži beskonačno mnogo prostih brojeva. 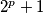 , a ne
, a ne 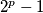 :D
:D 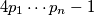 , tj.
, tj. 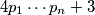 , pa nemaju odvojene slucajeve.
, pa nemaju odvojene slucajeve.