Točno
15. lipnja 2015. 12:48 (10 godine, 9 mjeseci)
Neka su

,

i

pozitivni realni brojevi takvi da je
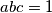
. Dokažite:
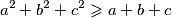
%V0
Neka su $a$, $b$ i $c$ pozitivni realni brojevi takvi da je $abc = 1$. Dokažite:
$$a^2 + b^2 + c^2 \geqslant a + b + c$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
Prema $A \geq G$
$\frac{a+b+c}{3} \geq \sqrt[3]{abc}$
Budući da $abc=1$
$a+b+c \geq 3\sqrt[3]1$
$a+b+c \geq 3$
Prema $K\geq A$
$\sqrt{\frac{a^2+b^2+c^2}{3}} \geq \frac{a+b+c}{3}$
$3\sqrt{\frac{a^2+b^2+c^2}{3}} \geq a+b+c$
Prema tranzitivnosti:
$3\sqrt{\frac{a^2+b^2+c^2}{3}} \geq 3$
Budući da su obje strane pozitivne, kvadrirajmo:
$9\frac{a^2+b^2+c^2}{3}\geq 9$
$\frac{a^2+b^2+c^2}{3} \geq 1$
Ako je $x \geq 1, x \geq \sqrt{x}$
Prema tome:
$\frac{a^2+b^2+c^2}{3} \geq \sqrt{\frac{a^2+b^2+c^2}{3}}$
Prema tranzitivnosti:
$\frac{a^2+b^2+c^2}{3} \geq \frac{a+b+c}{3}$
$a^2+b^2+c^2 \geq a+b+c$
$Q.E.D.$
| 14. lipnja 2015. 09:02 | ikicic | Točno |