Školjka

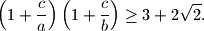
%V0 $(1+\frac{c}{a})(1+\frac{c}{b})\geq3+2\sqrt2$ $\frac{c}{a}+\frac{c}{b}+\frac{c^2}{ab}\geq2+2\sqrt2$ $\frac{c^2}{ab} = \frac{a^2+b^2}{ab}$ Prema $A \geq G$: $\frac{a^2+b^2}{2}\geq\sqrt{a^2b^2}$ $\frac{a^2+b^2}{2}\geq ab$ $\frac{a^2+b^2}{ab}\geq 2$ Prema $A \geq G$: $\frac{\frac{c}{a}+\frac{c}{b}}{2}\geq\sqrt{\frac{c}{a}\cdot\frac{c}{b}}$ $(\frac{\frac{c}{a}+\frac{c}{b}}{2})^2\geq\frac{c^2}{ab}$ $(\frac{\frac{c}{a}+\frac{c}{b}}{2})^2\geq\frac{a^2+b^2}{ab}$ Prema tranzitivnosti: $(\frac{\frac{c}{a}+\frac{c}{b}}{2})^2\geq2$ $\frac{c}{a}+\frac{c}{b}\geq2\sqrt2$ Zbrajajući nejednakosti: $\frac{c}{a}+\frac{c}{b}+\frac{a^2+b^2}{ab}\geq2+2\sqrt2$ $\frac{c}{a}+\frac{c}{b}+\frac{c^2}{ab}\geq2+2\sqrt2$ $Q.E.D.$