Točno
16. lipnja 2015. 20:28 (9 godine, 8 mjeseci)
Neka su
i
redom opseg i površina pravokutnika. Dokaži da vrijedi
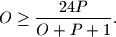
%V0
Neka su $O$ i $P$ redom opseg i površina pravokutnika. Dokaži da vrijedi $$
O\ge \dfrac{24P}{O+P+1}.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$O \geq \frac{24P}{O+P+1}$
$O^2 +OP+O \geq 24P$
$2(a+b)^2+ab(a+b)+a+b\geq12ab$
$2(a+b)^2+(ab+1)(a+b)\geq12ab$
Prema $A \geq G$:
$ab+1 \geq 2\sqrt{ab}$
Prema $A \geq G$:
$a+b \geq 2\sqrt{ab}$
Pa vrijedi i (jer su duljine stranica $a, b > 0$):
$2(a+b)^2 \geq 8ab$
Pomnožimo li prve dvije nejednakosti i dodamo treću:
$2(a+b)^2+(ab+1)(a+b)\geq12ab$
$Q.E.D.$
| 16. lipnja 2015. 17:23 | ikicic | Točno |
Školjka 
:
):
