Točno
16. lipnja 2015. 16:44 (9 godine, 8 mjeseci)
Odredi sve proste brojeve
za koje je
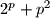
također prost broj.
%V0
Odredi sve proste brojeve $p$ za koje je $2^p+p^2$ također prost broj.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Ako je
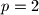
broj je
te nije prost.
Inače,
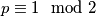
Prema tome:
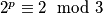
Ako je
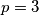
broj je
, prost je te je
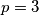
rješenje.
Inače:
Ako je
:
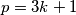
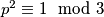
Ako je
:
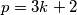
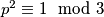
U oba slučaja,
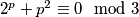
te nije prost, pa je
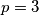
jedino rješenje.
%V0
Ako je $p=2$ broj je $8$ te nije prost.
Inače, $p \equiv 1\mod 2$
Prema tome:
$2^p \equiv 2\mod 3$
Ako je $p=3$ broj je $17$, prost je te je $p=3$ rješenje.
Inače:
Ako je $p = 3k+1$:
$p^2\equiv 1\mod 3$
Ako je $p=3k+2$:
$p^2\equiv 1\mod 3$
U oba slučaja, $2^p+p^2\equiv 0\mod 3$ te nije prost, pa je $p=3$ jedino rješenje.
| 16. lipnja 2015. 17:25 | ikicic | Točno |
Školjka