Točno
20. lipnja 2015. 01:01 (10 godine, 8 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.

Označimo sa
 skup ostataka brojeva
skup ostataka brojeva 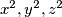 pri dijeljenju sa
pri dijeljenju sa  .
.Elementi skupa mogu biti samo
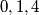 te zbroj svaka dva elementa u skupu smije biti samo jedan od tih brojeva.
te zbroj svaka dva elementa u skupu smije biti samo jedan od tih brojeva.Izostavljamo skupove koji sadrže
 , jer je za njih očito
, jer je za njih očito 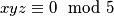 .
.Izostavljamo skupove koji dvaput sadrže
 ili dvaput sadrže
ili dvaput sadrže  jer
jer 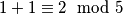 a
a 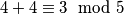 što nije dozvoljeno.
što nije dozvoljeno.Ups, više nemamo skupova.

Označimo sa
 skup ostataka brojeva
skup ostataka brojeva 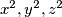 pri dijeljenju sa
pri dijeljenju sa  .
.Elementi skupa mogu biti samo
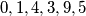 te zbroj svaka dva elementa u skupu smije biti samo jedan od tih brojeva.
te zbroj svaka dva elementa u skupu smije biti samo jedan od tih brojeva.Izostavljamo skupove koji sadrže
 , jer je za njih očito
, jer je za njih očito 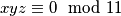 .
.Izostavljamo skupove koji dvaput sadrže
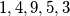 , jer ti zbrojevi ne daju lijep ostatak pri dijeljenju s
, jer ti zbrojevi ne daju lijep ostatak pri dijeljenju s  .
.Skupovi smiju sadržavati samo zbrojeve
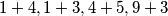 , nikakve druge, pa ne možemo sastaviti poželjan skup.
, nikakve druge, pa ne možemo sastaviti poželjan skup.Budući da su umnošci elemenata svih poželjnih skupova djeljivi i sa
 i sa
i sa  , svi su
, svi su 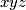 djeljivi s
djeljivi s 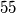 .
.  Školjka
Školjka 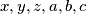 cijeli brojevi za koje vrijedi:
cijeli brojevi za koje vrijedi: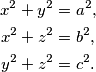 Dokažite da je broj
Dokažite da je broj 
