Točno
6. kolovoza 2012. 20:57 (13 godine, 6 mjeseci)
For each integer
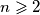
, determine the largest real constant
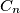
such that for all positive real numbers
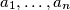
we have
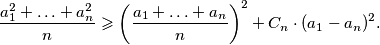
%V0
For each integer $n\geqslant2$, determine the largest real constant $C_n$ such that for all positive real numbers $a_1, \ldots, a_n$ we have $$\frac{a_1^2+\ldots+a_n^2}{n}\geqslant\left(\frac{a_1+\ldots+a_n}{n}\right)^2+C_n\cdot(a_1-a_n)^2\mbox{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Uvrstimo
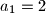
,
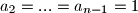
i
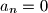
pa vidimo da je
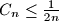
. Dokažimo nejednakost za
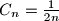
.
Neka je
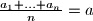
i
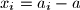
. Tada je očito
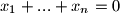
, a nejednakost je ekvivalentna s:
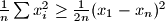
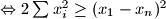
Što slijedi iz:
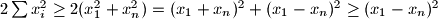
%V0
Uvrstimo $a_1=2$, $a_2=...=a_{n-1}=1$ i $a_n=0$ pa vidimo da je $C_n \leq \frac{1}{2n}$. Dokažimo nejednakost za $C_n = \frac{1}{2n}$.
Neka je $\frac{a_1+...+a_n}{n} =a$ i $x_i=a_i-a$. Tada je očito $x_1+...+x_n=0$, a nejednakost je ekvivalentna s:
$\frac{1}{n} \sum x_i^2 \ge \frac{1}{2n}(x_1-x_n)^2$
$\Leftrightarrow 2\sum x_i^2 \ge (x_1-x_n)^2$
Što slijedi iz:
$2\sum x_i^2 \ge 2(x_1^2+x_n^2)=(x_1+x_n)^2+(x_1-x_n)^2 \ge (x_1-x_n)^2$
| 16. prosinca 2012. 21:27 | grga | Točno |