Netočno
6. kolovoza 2012. 21:07 (13 godine, 6 mjeseci)
Dokažite da za sve realne brojeve
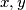
vrijedi nejednakost:
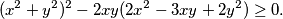
Kada vrijedi jednakost?
%V0
Dokažite da za sve realne brojeve $x, y$ vrijedi nejednakost: $$(x^2+y^2)^2-2xy(2x^2-3xy+2y^2)\geq0.$$ Kada vrijedi jednakost?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Najprije uočimo da je nejednakost ružna. (Nećemo dalje ništa zaključivati iz toga, samo uočimo.)
Očito je dovoljno dokazati nejednakost kad su oba pozitivna. U tom slučaju dokazat ćemo jaču nejednakost:
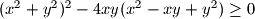
A ona slijedi iz jednostavne nejednakosti:
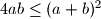
:
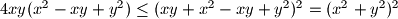
.
%V0
Najprije uočimo da je nejednakost ružna. (Nećemo dalje ništa zaključivati iz toga, samo uočimo.)
Očito je dovoljno dokazati nejednakost kad su oba pozitivna. U tom slučaju dokazat ćemo jaču nejednakost:
$(x^2+y^2)^2-4xy(x^2-xy+y^2) \ge 0$
A ona slijedi iz jednostavne nejednakosti: $4ab \leq (a+b)^2$:
$4xy(x^2-xy+y^2) \leq (xy+x^2-xy+y^2)^2 =(x^2+y^2)^2$.
| 16. prosinca 2012. 21:20 | grga | Netočno |