kdog, 8. kolovoza 2012. 09:32
@ikicic: Ups, da. Hvala na informaciji.
%V0
@ikicic: Ups, da. Hvala na informaciji.
ikicic, 8. kolovoza 2012. 03:48
Bulj, super rjesenje, bravo :D
@kdog:
Ovaj korak nije dobar:
Iz
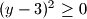
slijedi
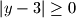
, sto nije neka prekorisna informacija. (kvadrat bilo kojeg broja je veci ili jednak

, ne mozes nista zakljuciti iz
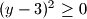
)
%V0
Bulj, super rjesenje, bravo :D
@kdog:
Ovaj korak nije dobar:
[quote]$(y - 3)^2 \geq 0 /^{\sqrt[]{}}$
$y - 3 \geq 0$
$y \geq 3$
[/quote]
Iz $(y-3)^2 \geq 0$ slijedi $|y-3| \geq 0$, sto nije neka prekorisna informacija. (kvadrat bilo kojeg broja je veci ili jednak $0$, ne mozes nista zakljuciti iz $(y-3)^2 \geq 0$)
Zadnja promjena:
ikicic, 14. kolovoza 2012. 19:31
kdog, 7. kolovoza 2012. 19:40
Ne znam šta ti znači ovo prvo.. Kako si zaključio da je
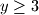
?
Hvala. :)
Btw jel se smije znati tko si ti? Mislim, znamo li se sa državnih?
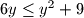
(iz AG nejednakosti)
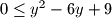
![(y - 3)^2 \geq 0 /^{\sqrt[]{}}](/media/m/6/e/d/6ed9ea9e2e7440088d9a5aa461edd757.png)
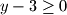
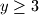
A
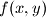
je koliko ja kužim kvadrat udaljenosti između

i

(
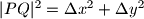
)?
I pretpostavljam da se ne znamo (ili se ne sjećam, prošlo je već nekih 3 ili više mj.)
%V0
[quote]Ne znam šta ti znači ovo prvo.. Kako si zaključio da je $y\ge 3$ ?
Hvala. :)
Btw jel se smije znati tko si ti? Mislim, znamo li se sa državnih?[/quote]
$6y \leq y^2 + 9$ (iz AG nejednakosti)
$0 \leq y^2 - 6y + 9$
$(y - 3)^2 \geq 0 /^{\sqrt[]{}}$
$y - 3 \geq 0$
$y \geq 3$
A $f(x, y)$ je koliko ja kužim kvadrat udaljenosti između $P$ i $Q$ ($|PQ|^2 = \Delta x^2 + \Delta y^2$)?
I pretpostavljam da se ne znamo (ili se ne sjećam, prošlo je već nekih 3 ili više mj.)
abulj, 7. kolovoza 2012. 18:16
Ne znam šta ti znači ovo prvo.. Kako si zaključio da je
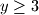
?
Hvala. :)
Btw jel se smije znati tko si ti? Mislim, znamo li se sa državnih?
%V0
Ne znam šta ti znači ovo prvo.. Kako si zaključio da je $y\ge 3$ ?
Hvala. :)
Btw jel se smije znati tko si ti? Mislim, znamo li se sa državnih?
Zadnja promjena:
abulj, 7. kolovoza 2012. 18:20
kdog, 7. kolovoza 2012. 17:33
Pretpostavljam
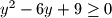
,
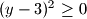
,
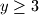
, te
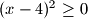
,
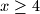
,
a onda dokaz da
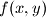
sa
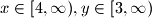
ima minimum za donje granice

i

? Wow.
Ja sam osobno išao pomoću diferencijalnog računa (i požalio), dobio jednadžbu 4 stupnja koja se da faktorizirati kao
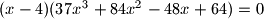
pa je
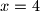
jedno realno rješenje, a drugo je negativno pa je tražena
točka očito
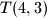
. Svaka čast na elementarnom rješenju.
%V0
Pretpostavljam
$y^2-6y+9 \geq 0$, $(y - 3)^2 \geq 0$, $y \geq 3$, te
$(x - 4)^2 \geq 0$, $x \geq 4$,
a onda dokaz da $f(x, y)$ sa $x \in [4, \infty), y\in [3, \infty)$ ima minimum za donje granice $x$ i $y$? Wow.
Ja sam osobno išao pomoću diferencijalnog računa (i požalio), dobio jednadžbu 4 stupnja koja se da faktorizirati kao $(x - 4)(37x^3 + 84x^2 - 48x + 64) = 0$ pa je $x = 4$ jedno realno rješenje, a drugo je negativno pa je tražena
točka očito $T(4, 3)$. Svaka čast na elementarnom rješenju.
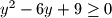 ,
, 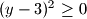 ,
, 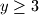 , te
, te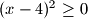 ,
, 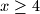 ,
,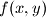 sa
sa 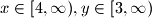 ima minimum za donje granice
ima minimum za donje granice  i
i  ? Wow.
? Wow.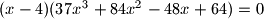 pa je
pa je 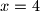 jedno realno rješenje, a drugo je negativno pa je tražena
jedno realno rješenje, a drugo je negativno pa je tražena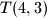 . Svaka čast na elementarnom rješenju.
. Svaka čast na elementarnom rješenju. 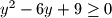 ,
, 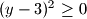 ,
, 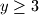 , te
, te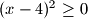 ,
, 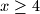 ,
,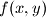 sa
sa 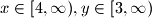 ima minimum za donje granice
ima minimum za donje granice  i
i  ? Wow.
? Wow.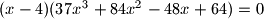 pa je
pa je 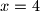 jedno realno rješenje, a drugo je negativno pa je tražena
jedno realno rješenje, a drugo je negativno pa je tražena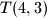 . Svaka čast na elementarnom rješenju.
. Svaka čast na elementarnom rješenju.  Školjka
Školjka 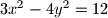 odredi točku najbližu točki
odredi točku najbližu točki 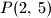 .
. 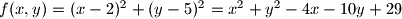
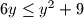 pa koristeći tu činjenicu i uvjet imamo:
pa koristeći tu činjenicu i uvjet imamo: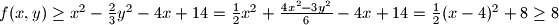
 .
. ![(y - 3)^2 \geq 0 /^{\sqrt[]{}}](/media/m/6/e/d/6ed9ea9e2e7440088d9a5aa461edd757.png)
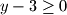
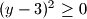 slijedi
slijedi 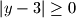 , sto nije neka prekorisna informacija. (kvadrat bilo kojeg broja je veci ili jednak
, sto nije neka prekorisna informacija. (kvadrat bilo kojeg broja je veci ili jednak  , ne mozes nista zakljuciti iz
, ne mozes nista zakljuciti iz 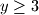 ?
?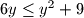 (iz AG nejednakosti)
(iz AG nejednakosti)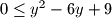
 i
i  (
(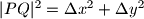 )?
)?