Točno
17. kolovoza 2012. 19:35 (13 godine, 5 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Promatrat cemo 5 slucajeva.
1
2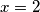
3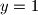
4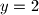
5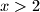 i
i 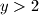
1.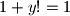
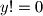 nema rjesenja
nema rjesenja
2.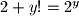
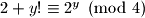 ako
ako 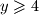 dobivamo
dobivamo 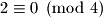 , dakle
, dakle 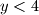
Provjerom dobivamo da su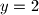 i
i 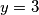 rjesenja.
rjesenja.
3.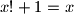
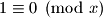 dakle jedino moguce rjesenja je
dakle jedino moguce rjesenja je  , a to ynamo da nema rjesenja.
, a to ynamo da nema rjesenja.
4.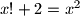
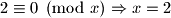
5.Iz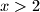 i
i 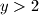 dobivamo
dobivamo 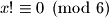 i
i 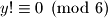 , pa zato i
, pa zato i 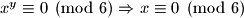
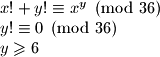
Neka je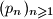 niz prostih brojeva.
niz prostih brojeva.
Pretpostavimo da smo dokazali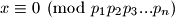 i
i 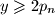
Znamo da postoji prost broj izmedi i
i  pa znamo da je
pa znamo da je 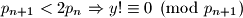
Takoder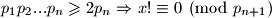

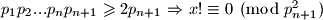
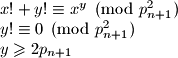
Dakle ovaj slucaj nema rjesenja.
Jedina rjesenja su uredeni parovi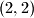 i
i 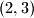
1

2
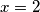
3
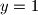
4
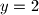
5
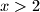 i
i 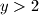
1.
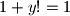
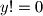 nema rjesenja
nema rjesenja2.
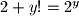
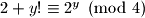 ako
ako 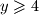 dobivamo
dobivamo 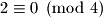 , dakle
, dakle 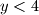
Provjerom dobivamo da su
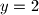 i
i 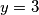 rjesenja.
rjesenja.3.
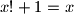
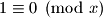 dakle jedino moguce rjesenja je
dakle jedino moguce rjesenja je  , a to ynamo da nema rjesenja.
, a to ynamo da nema rjesenja.4.
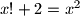
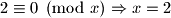
5.Iz
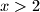 i
i 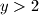 dobivamo
dobivamo 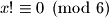 i
i 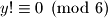 , pa zato i
, pa zato i 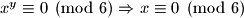
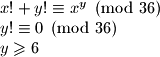
Neka je
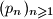 niz prostih brojeva.
niz prostih brojeva.Pretpostavimo da smo dokazali
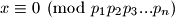 i
i 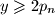
Znamo da postoji prost broj izmedi
 i
i  pa znamo da je
pa znamo da je 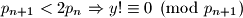
Takoder
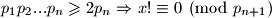

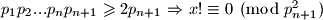
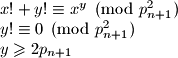
Dakle ovaj slucaj nema rjesenja.
Jedina rjesenja su uredeni parovi
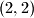 i
i 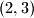
 Školjka
Školjka  of positive integers satisfying the equation
of positive integers satisfying the equation