Točno
17. kolovoza 2012. 22:35 (13 godine, 6 mjeseci)
A tetrahedron is called a MEMO-tetrahedron if all six sidelengths are different positive integers where one of them is  and one of them is
and one of them is  . Let
. Let 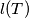 be the sum of the sidelengths of the tetrahedron
be the sum of the sidelengths of the tetrahedron  .
.
(a) Find all positive integers so that there exists a MEMO-Tetrahedron
so that there exists a MEMO-Tetrahedron  with
with 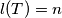 .
.
(b) How many pairwise non-congruent MEMO-tetrahedrons satisfying
satisfying 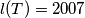 exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
 and one of them is
and one of them is  . Let
. Let 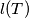 be the sum of the sidelengths of the tetrahedron
be the sum of the sidelengths of the tetrahedron  .
. (a) Find all positive integers
 so that there exists a MEMO-Tetrahedron
so that there exists a MEMO-Tetrahedron  with
with 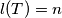 .
. (b) How many pairwise non-congruent MEMO-tetrahedrons
 satisfying
satisfying 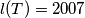 exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume). Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Promatrati cemo dva slucaja, kada su stranice duljina  I
I  u istome trokutu, i kada nisu.
u istome trokutu, i kada nisu.
U prvom slucaju imamo trokut sa stranicama i
i  pa iz nejednakosti trokuta dobivamo da je treca stranica (nazovimo je
pa iz nejednakosti trokuta dobivamo da je treca stranica (nazovimo je  )
)
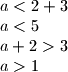
dakle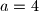
Neka je najmanja od preostale tri stranice tetraedra . Postoje tri mogucnosti iz kojega ce vrha
. Postoje tri mogucnosti iz kojega ce vrha  izlaziti.
izlaziti.
1. Ako postoji vrh sa stranicama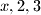 .
.
U trokutu sa stranicama i
i  je treca stranica
je treca stranica 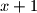 .
.
U trokutu sa stranicama i
i  treca stranica zato mora biti
treca stranica zato mora biti 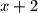 .
.
Dakle takvi tetraedri mogu imati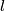 jedino oblika
jedino oblika 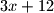
2.Ako postoji vrh sa stranicama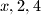
U trokutu sa stranicama i
i  zadnja je stranica
zadnja je stranica 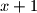 .
.
U trokutu sa stranicama i
i  posaljednja stranica sada moze biti
posaljednja stranica sada moze biti 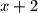 ili
ili 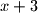 .
.
Dakle takvi tetraedri mogu imati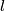 oblika
oblika 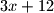 ili
ili 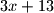 .
.
3. Ako postoji vrh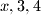
U trokutu sa stranicama i
i  zadnja je stranica ili
zadnja je stranica ili 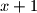 ili
ili 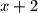 .
.
Neka je posljednja stranica u tetraedru . U trokutu imamo
. U trokutu imamo  i
i  , pa znamo da
, pa znamo da
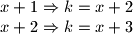 ili
ili 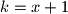 .
.
Dakle takvi tetraedri mogu imati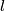 oblika
oblika 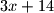 ili oblika
ili oblika 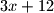 na dva nekongruentna nacina.
na dva nekongruentna nacina.
Drugi slucaj:stranice nisu u istom trokutu.
Neka je od preostalih stranica najmanja . U trokutu sa stranicama
. U trokutu sa stranicama  i
i  , posljednja stranica mora biti
, posljednja stranica mora biti 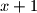 zbog nejednakosti trokuta. U trokutu sa stranicama
zbog nejednakosti trokuta. U trokutu sa stranicama  i
i  , posljednja stranica mora biti
, posljednja stranica mora biti 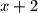 , jer nemoze biti
, jer nemoze biti 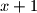 zbog uvjeta da su stranice razlicite. U trokutu sa stranicama
zbog uvjeta da su stranice razlicite. U trokutu sa stranicama 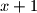 i
i  zadnja je stranica
zadnja je stranica 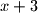 . Svi tetraedri u kojima
. Svi tetraedri u kojima  i
i  nisu u istom trokutu moraju biti ovoga oblika.
nisu u istom trokutu moraju biti ovoga oblika.
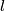 takvog tetraedra je oblika
takvog tetraedra je oblika 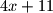 , a broj
, a broj  moguce je prikayati kao
moguce je prikayati kao 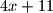 . Najmanji
. Najmanji 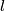 kojeg ovakav tetraedar moze poprimiti poprima se za
kojeg ovakav tetraedar moze poprimiti poprima se za 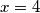 i jedank je
i jedank je 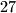 .
.
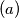 U prvom slucaju najmanji mogci
U prvom slucaju najmanji mogci 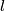 postize se za
postize se za 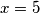 i jednak je
i jednak je 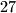 . Svi brojevi veci ili jednaki
. Svi brojevi veci ili jednaki 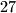 mogu se postici jer su zapisivi u obliku
mogu se postici jer su zapisivi u obliku 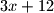 ili
ili 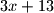 ili
ili 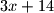 .
.
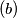 U prvom slucaju imamo 4 nekongruentna nacina na koje mozemo napraviti tetraedar
U prvom slucaju imamo 4 nekongruentna nacina na koje mozemo napraviti tetraedar  takav da
takav da 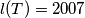 , a moguce je i na jedan nacin iz drugog slucaja pa ukupno postoji
, a moguce je i na jedan nacin iz drugog slucaja pa ukupno postoji 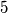 takvih nekongruentnih tetraedara.
takvih nekongruentnih tetraedara.
 I
I  u istome trokutu, i kada nisu.
u istome trokutu, i kada nisu.U prvom slucaju imamo trokut sa stranicama
 i
i  pa iz nejednakosti trokuta dobivamo da je treca stranica (nazovimo je
pa iz nejednakosti trokuta dobivamo da je treca stranica (nazovimo je  )
)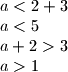
dakle
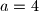
Neka je najmanja od preostale tri stranice tetraedra
 . Postoje tri mogucnosti iz kojega ce vrha
. Postoje tri mogucnosti iz kojega ce vrha  izlaziti.
izlaziti.1. Ako postoji vrh sa stranicama
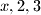 .
.U trokutu sa stranicama
 i
i  je treca stranica
je treca stranica 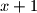 .
.U trokutu sa stranicama
 i
i  treca stranica zato mora biti
treca stranica zato mora biti 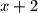 .
.Dakle takvi tetraedri mogu imati
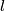 jedino oblika
jedino oblika 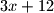
2.Ako postoji vrh sa stranicama
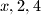
U trokutu sa stranicama
 i
i  zadnja je stranica
zadnja je stranica 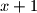 .
.U trokutu sa stranicama
 i
i  posaljednja stranica sada moze biti
posaljednja stranica sada moze biti 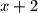 ili
ili 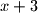 .
.Dakle takvi tetraedri mogu imati
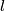 oblika
oblika 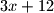 ili
ili 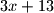 .
.3. Ako postoji vrh
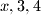
U trokutu sa stranicama
 i
i  zadnja je stranica ili
zadnja je stranica ili 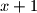 ili
ili 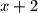 .
.Neka je posljednja stranica u tetraedru
 . U trokutu imamo
. U trokutu imamo  i
i  , pa znamo da
, pa znamo da 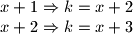 ili
ili 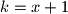 .
.Dakle takvi tetraedri mogu imati
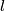 oblika
oblika 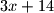 ili oblika
ili oblika 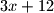 na dva nekongruentna nacina.
na dva nekongruentna nacina.Drugi slucaj:stranice nisu u istom trokutu.
Neka je od preostalih stranica najmanja
 . U trokutu sa stranicama
. U trokutu sa stranicama  i
i  , posljednja stranica mora biti
, posljednja stranica mora biti 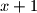 zbog nejednakosti trokuta. U trokutu sa stranicama
zbog nejednakosti trokuta. U trokutu sa stranicama  i
i  , posljednja stranica mora biti
, posljednja stranica mora biti 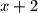 , jer nemoze biti
, jer nemoze biti 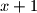 zbog uvjeta da su stranice razlicite. U trokutu sa stranicama
zbog uvjeta da su stranice razlicite. U trokutu sa stranicama 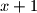 i
i  zadnja je stranica
zadnja je stranica 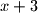 . Svi tetraedri u kojima
. Svi tetraedri u kojima  i
i  nisu u istom trokutu moraju biti ovoga oblika.
nisu u istom trokutu moraju biti ovoga oblika.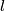 takvog tetraedra je oblika
takvog tetraedra je oblika 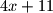 , a broj
, a broj 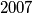 moguce je prikayati kao
moguce je prikayati kao 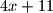 . Najmanji
. Najmanji 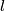 kojeg ovakav tetraedar moze poprimiti poprima se za
kojeg ovakav tetraedar moze poprimiti poprima se za 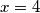 i jedank je
i jedank je 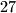 .
. U prvom slucaju najmanji mogci
U prvom slucaju najmanji mogci 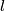 postize se za
postize se za 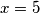 i jednak je
i jednak je 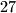 . Svi brojevi veci ili jednaki
. Svi brojevi veci ili jednaki 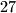 mogu se postici jer su zapisivi u obliku
mogu se postici jer su zapisivi u obliku 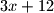 ili
ili 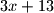 ili
ili 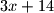 .
.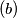 U prvom slucaju imamo 4 nekongruentna nacina na koje mozemo napraviti tetraedar
U prvom slucaju imamo 4 nekongruentna nacina na koje mozemo napraviti tetraedar  takav da
takav da 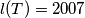 , a moguce je i na jedan nacin iz drugog slucaja pa ukupno postoji
, a moguce je i na jedan nacin iz drugog slucaja pa ukupno postoji 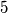 takvih nekongruentnih tetraedara.
takvih nekongruentnih tetraedara.  Školjka
Školjka