Točno
5. kolovoza 2015. 14:40 (10 godine, 7 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo da neki n zadovoljava te uvjete. Tada zbog (a) sigurno postoje barem 2 djeljitelja broja n veca od 1 a manja od n.
Neka je a najmanji djeljitelj broja n veci od 1, a b drugi najmanji. Ocigledno, a mora biti prost.
Sada ne posotji broj c takav da je 1 < c < a ili a < c < b a da dijeli n.
A ipak, c = b - a < b more dijeliti n. Stoga imamo dva slucaja:
1. c = a
Tada vrijedi b = 2a sto znaci da 2 dijeli n pa je a = 2 jer je 2 najmanji prosti broj.
Dalje slijedi b = 4 te 4 | n
Sada je lako za uociti da je n = 8 jedno od rjesenja, a sve potencije broja 2 vece od 8 nisu, jer bi to znacilo da i 2 i 8 dijele n, a 6 ne dijeli sto je kontrdikcija!
Pretpostavimo da je p najmanji neparni prosti djeljitelj broja n
Kako 2 | n mora vrijediti x = p - 2 | n, sto nemoguce, jer x mora biti neparan, a ne moze biti 1 jer bi tada x = 3 | n pa bi b morao biti 3 sto nije moguce ( u ovom slucaju ) , ne moze biti prost broj jer vrijedi x < p a p je najmanji prost broj, niti moze biti slozen jer bi to znacilo da postoji barem jedan jos manji neparni prost broj.
Dakle, u ovom slucaju jedino je rjesenje n = 8
2. c = 1
Sada i b mora biti prost, inace b = a ^ 2 pa je c = b - a = a * ( a - 1 ) >= 2 * 1 > 1 =><=
Sada je b - a = 1, pa mora biti a = 2 te b = 3. Sada je ocigledno rjesenje 6.
Pretpostavimo n > 6. Tada vrijedi n >= 12
Sada mora biti 4 | n jer 2 i 6 ( jer 2 i 3 dijele n ) dijele n,
pa dalje 8 | n jer 4 i 12 ( jer 4 i 3 dijele n ) dijele n,
pa 16 | n itd.
Zakljucujemo da bi tada n morao imati beskonacno mnogo prostih faktora 2 u svojem rastavu ( lako dokazivo indukcijom ) , stoga je n = 6 jedino rjesenje ovog slucaja.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------
Dakle jedina rjesenja su 6 i 8.
Neka je a najmanji djeljitelj broja n veci od 1, a b drugi najmanji. Ocigledno, a mora biti prost.
Sada ne posotji broj c takav da je 1 < c < a ili a < c < b a da dijeli n.
A ipak, c = b - a < b more dijeliti n. Stoga imamo dva slucaja:
1. c = a
Tada vrijedi b = 2a sto znaci da 2 dijeli n pa je a = 2 jer je 2 najmanji prosti broj.
Dalje slijedi b = 4 te 4 | n
Sada je lako za uociti da je n = 8 jedno od rjesenja, a sve potencije broja 2 vece od 8 nisu, jer bi to znacilo da i 2 i 8 dijele n, a 6 ne dijeli sto je kontrdikcija!
Pretpostavimo da je p najmanji neparni prosti djeljitelj broja n
Kako 2 | n mora vrijediti x = p - 2 | n, sto nemoguce, jer x mora biti neparan, a ne moze biti 1 jer bi tada x = 3 | n pa bi b morao biti 3 sto nije moguce ( u ovom slucaju ) , ne moze biti prost broj jer vrijedi x < p a p je najmanji prost broj, niti moze biti slozen jer bi to znacilo da postoji barem jedan jos manji neparni prost broj.
Dakle, u ovom slucaju jedino je rjesenje n = 8
2. c = 1
Sada i b mora biti prost, inace b = a ^ 2 pa je c = b - a = a * ( a - 1 ) >= 2 * 1 > 1 =><=
Sada je b - a = 1, pa mora biti a = 2 te b = 3. Sada je ocigledno rjesenje 6.
Pretpostavimo n > 6. Tada vrijedi n >= 12
Sada mora biti 4 | n jer 2 i 6 ( jer 2 i 3 dijele n ) dijele n,
pa dalje 8 | n jer 4 i 12 ( jer 4 i 3 dijele n ) dijele n,
pa 16 | n itd.
Zakljucujemo da bi tada n morao imati beskonacno mnogo prostih faktora 2 u svojem rastavu ( lako dokazivo indukcijom ) , stoga je n = 6 jedino rjesenje ovog slucaja.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------
Dakle jedina rjesenja su 6 i 8.
Ocjene: (1)
Komentari:
grga, 31. kolovoza 2015. 00:49
 Školjka
Školjka  which satisfy the following tow conditions:
which satisfy the following tow conditions: and
and  of
of 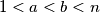 , the number
, the number 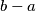 divides
divides 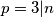 ...", dakle samo
...", dakle samo  umjesto
umjesto 
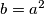 . potpuno nebitno, ali da
. potpuno nebitno, ali da