Točno
16. rujna 2015. 17:11 (8 godine, 7 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Prosta faktorizacija broja  je
je 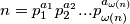 . Radi multiplikativnosti funkcije
. Radi multiplikativnosti funkcije 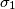 za relativno proste brojeve:
za relativno proste brojeve:
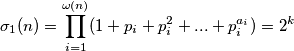
Iz ovoga možemo zaključiti da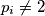 te da
te da 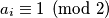 .
.
Također, za svaki možemo reći
možemo reći 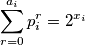
Promatrajmo neki od njih:
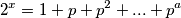
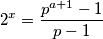
Ako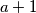 ima nekog neparnog djelitelja
ima nekog neparnog djelitelja  :
:
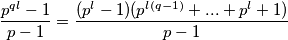
Tada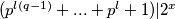 (jer očito
(jer očito 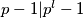 ) što je nemoguće jer je to neparan broj različit od
) što je nemoguće jer je to neparan broj različit od  .
.
Prema tome, očito je da je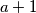 potencija broja
potencija broja  .
.
Ako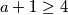 ,
, 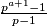 se očito može zapisati kao
se očito može zapisati kao 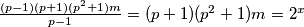 , ali to nije moguće jer
, ali to nije moguće jer 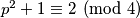 a
a 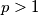 pa
pa 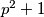 ima neparne proste djelitelje.
ima neparne proste djelitelje.
Zbog toga,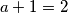 pa
pa 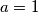 .
.
Slijedi:
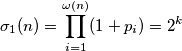
Iz ovoga je očito da je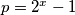 tj. da je svaki
tj. da je svaki  Mersenne prost broj (jer je trivijalno dokazivo da je
Mersenne prost broj (jer je trivijalno dokazivo da je  nužno prost) te možemo reći da
nužno prost) te možemo reći da  mora biti umnožak različitih (jer je svaki
mora biti umnožak različitih (jer je svaki 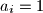 ) Mersenne prostih brojeva ili i sam Mersenne prost broj. Lako je vidljivo da je taj uvjet i dovoljan.
) Mersenne prostih brojeva ili i sam Mersenne prost broj. Lako je vidljivo da je taj uvjet i dovoljan.
 je
je 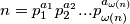 . Radi multiplikativnosti funkcije
. Radi multiplikativnosti funkcije 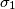 za relativno proste brojeve:
za relativno proste brojeve: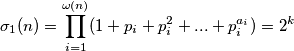
Iz ovoga možemo zaključiti da
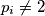 te da
te da 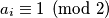 .
.Također, za svaki
 možemo reći
možemo reći 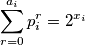
Promatrajmo neki od njih:
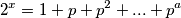
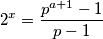
Ako
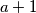 ima nekog neparnog djelitelja
ima nekog neparnog djelitelja  :
: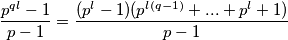
Tada
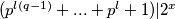 (jer očito
(jer očito 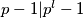 ) što je nemoguće jer je to neparan broj različit od
) što je nemoguće jer je to neparan broj različit od  .
.Prema tome, očito je da je
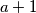 potencija broja
potencija broja  .
. Ako
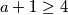 ,
, 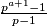 se očito može zapisati kao
se očito može zapisati kao 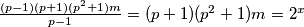 , ali to nije moguće jer
, ali to nije moguće jer 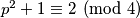 a
a 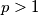 pa
pa 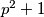 ima neparne proste djelitelje.
ima neparne proste djelitelje. Zbog toga,
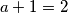 pa
pa 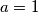 .
.Slijedi:
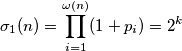
Iz ovoga je očito da je
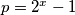 tj. da je svaki
tj. da je svaki  Mersenne prost broj (jer je trivijalno dokazivo da je
Mersenne prost broj (jer je trivijalno dokazivo da je  nužno prost) te možemo reći da
nužno prost) te možemo reći da  mora biti umnožak različitih (jer je svaki
mora biti umnožak različitih (jer je svaki 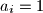 ) Mersenne prostih brojeva ili i sam Mersenne prost broj. Lako je vidljivo da je taj uvjet i dovoljan.
) Mersenne prostih brojeva ili i sam Mersenne prost broj. Lako je vidljivo da je taj uvjet i dovoljan. Ocjene: (1)
Komentari:
matsimic, 16. rujna 2015. 19:15
Puno hvala na dugom i promišljenom odgovoru. :D
Slažem se da ovo nije zadatak natjecateljskog tipa - jedino mjesto gdje sam kasnije vidio neku varijantu ovoga je neki američki matematički časopis koji je iskočio na Googleu, a tamo je postavljen kao "Prove that the sum of positive divisors of a natural number is a power of
is a power of  in and only if
in and only if  is a product of distinct Mersenne primes." što mi se činilo kao dobaar zapis, makar daje malo veći hint o rješenju te bi se tada cijeli zadatak u biti mogao rješiti oslanjajući se na to da je
is a product of distinct Mersenne primes." što mi se činilo kao dobaar zapis, makar daje malo veći hint o rješenju te bi se tada cijeli zadatak u biti mogao rješiti oslanjajući se na to da je 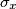 multiplikativna za relativno proste brojeve i provjeravajući što se dogodi ako broj koji zadovoljava uvjet pomnožimo sa bilo kojim prostim brojem koji to ne zadovoljava. Ljepota same karakterizacije je subjektivna i većinom ovisi o tome koliko je onaj koji rješava susretao Mersenne proste brojeve te bi li prepoznao rješenja za taj skup.
multiplikativna za relativno proste brojeve i provjeravajući što se dogodi ako broj koji zadovoljava uvjet pomnožimo sa bilo kojim prostim brojem koji to ne zadovoljava. Ljepota same karakterizacije je subjektivna i većinom ovisi o tome koliko je onaj koji rješava susretao Mersenne proste brojeve te bi li prepoznao rješenja za taj skup.
Definitvno stoji ovo što si rekao za zadatke "open problem" tipa gdje nema neko osobito "lijepo" rješenje, jer se time u biti provjerava i to koliko je onaj koji rješava siguran u svoje postupke i metode rješavanja i s njima upoznat ili samo ponavlja ono što je prije vidio ili primjenjivao dok ne dobije neko rješenje koje izgleda mogućim. Jedna moguća postava bi bila "Kakvi moraju biti prosti faktori broja ako je njegov zbroj djelitelja potencija broja
ako je njegov zbroj djelitelja potencija broja  ?"
?"
Sve u svemu, hvala na komentaru. :)
Slažem se da ovo nije zadatak natjecateljskog tipa - jedino mjesto gdje sam kasnije vidio neku varijantu ovoga je neki američki matematički časopis koji je iskočio na Googleu, a tamo je postavljen kao "Prove that the sum of positive divisors of a natural number
 is a power of
is a power of  in and only if
in and only if  is a product of distinct Mersenne primes." što mi se činilo kao dobaar zapis, makar daje malo veći hint o rješenju te bi se tada cijeli zadatak u biti mogao rješiti oslanjajući se na to da je
is a product of distinct Mersenne primes." što mi se činilo kao dobaar zapis, makar daje malo veći hint o rješenju te bi se tada cijeli zadatak u biti mogao rješiti oslanjajući se na to da je 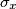 multiplikativna za relativno proste brojeve i provjeravajući što se dogodi ako broj koji zadovoljava uvjet pomnožimo sa bilo kojim prostim brojem koji to ne zadovoljava. Ljepota same karakterizacije je subjektivna i većinom ovisi o tome koliko je onaj koji rješava susretao Mersenne proste brojeve te bi li prepoznao rješenja za taj skup.
multiplikativna za relativno proste brojeve i provjeravajući što se dogodi ako broj koji zadovoljava uvjet pomnožimo sa bilo kojim prostim brojem koji to ne zadovoljava. Ljepota same karakterizacije je subjektivna i većinom ovisi o tome koliko je onaj koji rješava susretao Mersenne proste brojeve te bi li prepoznao rješenja za taj skup. Definitvno stoji ovo što si rekao za zadatke "open problem" tipa gdje nema neko osobito "lijepo" rješenje, jer se time u biti provjerava i to koliko je onaj koji rješava siguran u svoje postupke i metode rješavanja i s njima upoznat ili samo ponavlja ono što je prije vidio ili primjenjivao dok ne dobije neko rješenje koje izgleda mogućim. Jedna moguća postava bi bila "Kakvi moraju biti prosti faktori broja
 ako je njegov zbroj djelitelja potencija broja
ako je njegov zbroj djelitelja potencija broja  ?"
?"Sve u svemu, hvala na komentaru. :)
Zadnja promjena: matsimic, 16. rujna 2015. 20:23
grga, 16. rujna 2015. 18:37
Ok, fora, svidja mi se.
Ipak, postoji jedna stvar koju bih ti htio iskomentirat.
Ovo "nuzan i dovoljni uvjet" cu zvat "karakterizacija" jer mi je tako krace.
Dakle, tvoja karakterizacija trazenog skupa su svi brojevi koji su umnozak razlicitih Mersenovih prostih. Postavlja se pitanje koliko je ta karakterizacija bolja od pocetne? Dakle, koliko je "bolje" da ja kazem
 "to su svi
"to su svi  takvi da je
takvi da je 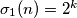 za neki
za neki  "
"
od toga da kazem, to
 "to su svi
"to su svi  takvi da oni u kanonskom rastavu glase
takvi da oni u kanonskom rastavu glase 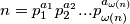 , pri cemu su svi
, pri cemu su svi 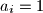 , te svi
, te svi  oblika
oblika 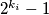 za neki
za neki 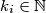 "??
"??
Sad, naravno, ovo je filozofsko pitanje i nema tocan odgovor. Kad bi npr odgovor na tvoje pitanje bio "svi prosti brojevi", onda bi se vjerojatno svi slozili da je to bolja karakterizacija. ili npr ako bi odgovor bio "brojevi 1, 2, 5 i 1727", to bi opet bila "bolja" karakterizacija. (ili da je odg svi parni brojevi, ili potencije broja 3 ili kako god).
Problem je u tome sto nema neki uniformni popis skupova koji bi se smatrao "normalnima/lijepima/osnovnima", pa onda ako je odgovor da je karakterizacija skupa iz zadatka jedan od tih skupova, onda je taj odgovor tocan ako ne onda nije.
Konkretno, osobno smatram da na natjecanjima nije moguce da dode ovaakav zadatak jer se skup Mersenovih brojeva (a kamoli onda onih ciji su svi prosti faktori jednostruki i Mersenovi) ne smatra "lijepim, osnovnim" skupom. Mozda je razlog tomu sto se ne ocekuje da svatko zna da taj skup postoji, pa onda jednom kad svede tvoj zadatak na daljnju karakterizaciju prostih brojeva oblika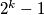 za neki prirodni
za neki prirodni  , taj netko ce misliti da je zapeo i traziti daljnju "ljepsu" karakterizaciju za taj skup iako ona zasad nije poznata matematickom svijetu (ili je mozda cak dokazano da ne postoji, sta god bi to znacilo, nebitno sada).
, taj netko ce misliti da je zapeo i traziti daljnju "ljepsu" karakterizaciju za taj skup iako ona zasad nije poznata matematickom svijetu (ili je mozda cak dokazano da ne postoji, sta god bi to znacilo, nebitno sada).
Npr, da si htio postaviti zadatak natjecateljskog tipa mogao si postaviti ovako nesto: "Ako je prost i vrijedi
prost i vrijedi 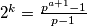 , za neki prirodan
, za neki prirodan  , dokazi da je
, dokazi da je 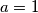 "
"
Sve u svemu, zadatak je dobar i drago mi je da je neko postavio zadatak za koji, jednom kad se dode do rjesenja, nije ocito da je bas to rjesenje.. tj zadatak "open problem" tipa, a ne jos jedan od natjecateljskih zadataka. meni je osobno u zadnje vrijeme dosta draze rjesavati takve zadatke za koje neznam imaju li "lijepo" rjesenje (ili, imaju li rjesenje uopce) od onih "normalnih". a i mislio sam da bi mozda tebe i druge interesirao ovaj problem sa karakterizacijom skupova i odredivanjem koji su skupovi "osnovni/lijepi", a koji nisu. Hvala na zadatku :)
Ipak, postoji jedna stvar koju bih ti htio iskomentirat.
Ovo "nuzan i dovoljni uvjet" cu zvat "karakterizacija" jer mi je tako krace.
Dakle, tvoja karakterizacija trazenog skupa su svi brojevi koji su umnozak razlicitih Mersenovih prostih. Postavlja se pitanje koliko je ta karakterizacija bolja od pocetne? Dakle, koliko je "bolje" da ja kazem
 "to su svi
"to su svi  takvi da je
takvi da je 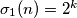 za neki
za neki  "
"od toga da kazem, to
 "to su svi
"to su svi  takvi da oni u kanonskom rastavu glase
takvi da oni u kanonskom rastavu glase 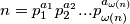 , pri cemu su svi
, pri cemu su svi 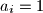 , te svi
, te svi  oblika
oblika 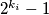 za neki
za neki 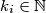 "??
"??Sad, naravno, ovo je filozofsko pitanje i nema tocan odgovor. Kad bi npr odgovor na tvoje pitanje bio "svi prosti brojevi", onda bi se vjerojatno svi slozili da je to bolja karakterizacija. ili npr ako bi odgovor bio "brojevi 1, 2, 5 i 1727", to bi opet bila "bolja" karakterizacija. (ili da je odg svi parni brojevi, ili potencije broja 3 ili kako god).
Problem je u tome sto nema neki uniformni popis skupova koji bi se smatrao "normalnima/lijepima/osnovnima", pa onda ako je odgovor da je karakterizacija skupa iz zadatka jedan od tih skupova, onda je taj odgovor tocan ako ne onda nije.
Konkretno, osobno smatram da na natjecanjima nije moguce da dode ovaakav zadatak jer se skup Mersenovih brojeva (a kamoli onda onih ciji su svi prosti faktori jednostruki i Mersenovi) ne smatra "lijepim, osnovnim" skupom. Mozda je razlog tomu sto se ne ocekuje da svatko zna da taj skup postoji, pa onda jednom kad svede tvoj zadatak na daljnju karakterizaciju prostih brojeva oblika
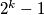 za neki prirodni
za neki prirodni  , taj netko ce misliti da je zapeo i traziti daljnju "ljepsu" karakterizaciju za taj skup iako ona zasad nije poznata matematickom svijetu (ili je mozda cak dokazano da ne postoji, sta god bi to znacilo, nebitno sada).
, taj netko ce misliti da je zapeo i traziti daljnju "ljepsu" karakterizaciju za taj skup iako ona zasad nije poznata matematickom svijetu (ili je mozda cak dokazano da ne postoji, sta god bi to znacilo, nebitno sada).Npr, da si htio postaviti zadatak natjecateljskog tipa mogao si postaviti ovako nesto: "Ako je
 prost i vrijedi
prost i vrijedi 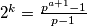 , za neki prirodan
, za neki prirodan  , dokazi da je
, dokazi da je 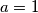 "
"Sve u svemu, zadatak je dobar i drago mi je da je neko postavio zadatak za koji, jednom kad se dode do rjesenja, nije ocito da je bas to rjesenje.. tj zadatak "open problem" tipa, a ne jos jedan od natjecateljskih zadataka. meni je osobno u zadnje vrijeme dosta draze rjesavati takve zadatke za koje neznam imaju li "lijepo" rjesenje (ili, imaju li rjesenje uopce) od onih "normalnih". a i mislio sam da bi mozda tebe i druge interesirao ovaj problem sa karakterizacijom skupova i odredivanjem koji su skupovi "osnovni/lijepi", a koji nisu. Hvala na zadatku :)
 Školjka
Školjka 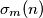 označava sumu
označava sumu  -tih potencija pozitivnih djelitelja broja
-tih potencija pozitivnih djelitelja broja