Točno
11. rujna 2015. 14:31 (10 godine, 4 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
prvo, primjetimo da je 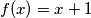 rjesenje.
rjesenje.
zato, uvedimo supstituciju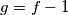 , imamo dakle
, imamo dakle
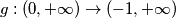
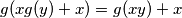
zelimo pokazati da je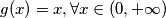
neka je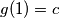
uvrstimo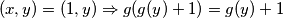
uvrstimo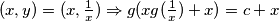
iz prethodna dva identiteta vidimo da je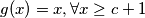
(to se vidi jer, uzmimo proizvoljan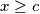 .. on je u slici funckije zbog drugog identiteta, tj postoji neki
.. on je u slici funckije zbog drugog identiteta, tj postoji neki  t.d. je
t.d. je 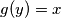 , tj, posebno ako je bas
, tj, posebno ako je bas  , onda smo oznacili
, onda smo oznacili 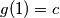 , a ako je
, a ako je  , onda vrijedi ovo zbog drugog identiteta. sad naprosto taj konkretan
, onda vrijedi ovo zbog drugog identiteta. sad naprosto taj konkretan  stavimo u prvi identitet pa dobivamo
stavimo u prvi identitet pa dobivamo 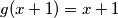 , sto smo i zeljeli pokazati)
, sto smo i zeljeli pokazati)
po dokazanom, vrijedi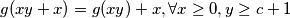 .
.
sad slijedi ideja za dokaz ostatka a zatim ide i formalni dio: (ako sad nastimamo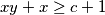 , ali
, ali 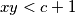 , onda cemo i za broj
, onda cemo i za broj 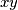 imati da je na njemu
imati da je na njemu 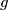 identiteta. tako cemo lako dobiti da je
identiteta. tako cemo lako dobiti da je 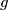 identiteta za sve brojeve vece od nekog
identiteta za sve brojeve vece od nekog 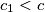 , te cemo nastavljanjem pokriti sve brojeve)
, te cemo nastavljanjem pokriti sve brojeve)
formalno, oznacimo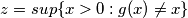 (dakle
(dakle  nam je "najveci" broj za kojeg
nam je "najveci" broj za kojeg 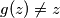 , s tim da se to nemora postizati nuzno za broj
, s tim da se to nemora postizati nuzno za broj  , npr ako bi
, npr ako bi 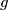 bila
bila  na brojevima
na brojevima 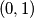 , a onda identiteta na brojevima
, a onda identiteta na brojevima 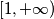 , tada bi bilo
, tada bi bilo 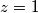 iako
iako  ).
).
uvrstimo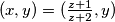 , pri cemu
, pri cemu 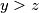 . tada imamo
. tada imamo
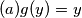
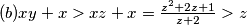
zbog imamo,
imamo, 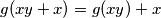 ,
,
sada zbog imamo
imamo 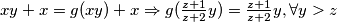
zadnji identitet nam govori da je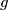 identiteta na brojevima vecim od
identiteta na brojevima vecim od 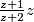 ,
,
drugim rjecima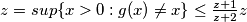 .
.
ovo naravno nije moguce ako je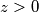 , pa zakljucujemo da je skup
, pa zakljucujemo da je skup 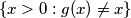 prazan. (u suprotnom, ako je neki
prazan. (u suprotnom, ako je neki 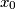 u tom skupu, po definiciji
u tom skupu, po definiciji 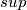 bit ce
bit ce 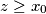 ).
).
kako je taj skup prazan, vrijedi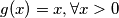 sto smo i zeljeli pokazati.
sto smo i zeljeli pokazati.
dakle, jedino moguce rjesenje je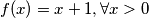 , a jednostavnom provjerom se vidi da to zaista i jest rjesenje.
, a jednostavnom provjerom se vidi da to zaista i jest rjesenje.
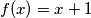 rjesenje.
rjesenje.zato, uvedimo supstituciju
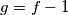 , imamo dakle
, imamo dakle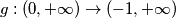
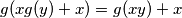
zelimo pokazati da je
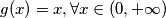
neka je
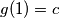
uvrstimo
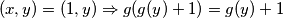
uvrstimo
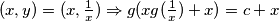
iz prethodna dva identiteta vidimo da je
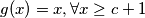
(to se vidi jer, uzmimo proizvoljan
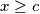 .. on je u slici funckije zbog drugog identiteta, tj postoji neki
.. on je u slici funckije zbog drugog identiteta, tj postoji neki  t.d. je
t.d. je 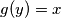 , tj, posebno ako je bas
, tj, posebno ako je bas  , onda smo oznacili
, onda smo oznacili 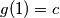 , a ako je
, a ako je  , onda vrijedi ovo zbog drugog identiteta. sad naprosto taj konkretan
, onda vrijedi ovo zbog drugog identiteta. sad naprosto taj konkretan  stavimo u prvi identitet pa dobivamo
stavimo u prvi identitet pa dobivamo 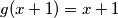 , sto smo i zeljeli pokazati)
, sto smo i zeljeli pokazati)po dokazanom, vrijedi
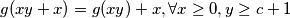 .
.sad slijedi ideja za dokaz ostatka a zatim ide i formalni dio: (ako sad nastimamo
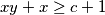 , ali
, ali 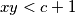 , onda cemo i za broj
, onda cemo i za broj 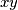 imati da je na njemu
imati da je na njemu 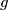 identiteta. tako cemo lako dobiti da je
identiteta. tako cemo lako dobiti da je 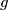 identiteta za sve brojeve vece od nekog
identiteta za sve brojeve vece od nekog 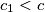 , te cemo nastavljanjem pokriti sve brojeve)
, te cemo nastavljanjem pokriti sve brojeve)formalno, oznacimo
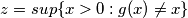 (dakle
(dakle  nam je "najveci" broj za kojeg
nam je "najveci" broj za kojeg 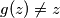 , s tim da se to nemora postizati nuzno za broj
, s tim da se to nemora postizati nuzno za broj  , npr ako bi
, npr ako bi 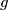 bila
bila  na brojevima
na brojevima 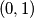 , a onda identiteta na brojevima
, a onda identiteta na brojevima 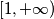 , tada bi bilo
, tada bi bilo 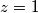 iako
iako  ).
).uvrstimo
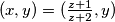 , pri cemu
, pri cemu 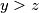 . tada imamo
. tada imamo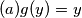
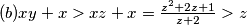
zbog
 imamo,
imamo, 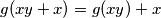 ,
,sada zbog
 imamo
imamo 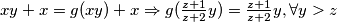
zadnji identitet nam govori da je
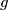 identiteta na brojevima vecim od
identiteta na brojevima vecim od 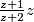 ,
,drugim rjecima
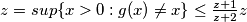 .
.ovo naravno nije moguce ako je
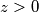 , pa zakljucujemo da je skup
, pa zakljucujemo da je skup 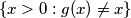 prazan. (u suprotnom, ako je neki
prazan. (u suprotnom, ako je neki 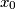 u tom skupu, po definiciji
u tom skupu, po definiciji 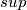 bit ce
bit ce 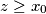 ).
).kako je taj skup prazan, vrijedi
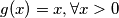 sto smo i zeljeli pokazati.
sto smo i zeljeli pokazati.dakle, jedino moguce rjesenje je
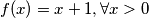 , a jednostavnom provjerom se vidi da to zaista i jest rjesenje.
, a jednostavnom provjerom se vidi da to zaista i jest rjesenje. Ocjene: (1)
Komentari:
grga, 28. listopada 2015. 13:33
ma da, naravno. ovaj formalni dio na kraju je skroz ruzan i zapravo nepotreban jer je jasno sta ce na kraju bit al sam htio napisat pa nek stoji :) a zato sam dao ono kvazi-objasnjenje gore ako se nekom neda citat to nastimavanje.
Hard core rješenje, svaka čast.
Pretpostavljam da kad si došao do onoga da je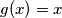 za svaki
za svaki 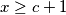 , da si znao da ćeš prije ili poslije dokazati tvrdnju i za ostale
, da si znao da ćeš prije ili poslije dokazati tvrdnju i za ostale  -eve?
-eve?
Pretpostavljam da kad si došao do onoga da je
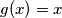 za svaki
za svaki 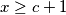 , da si znao da ćeš prije ili poslije dokazati tvrdnju i za ostale
, da si znao da ćeš prije ili poslije dokazati tvrdnju i za ostale  -eve?
-eve?ikicic, 14. listopada 2015. 20:26
 Školjka
Školjka 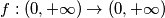 takve da za sve
takve da za sve 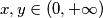 vrijedi
vrijedi