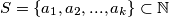
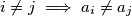
Dokaži da za svaki takav da postoji beskonačno mnogo takvih da
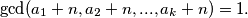
%V0
Dokaži da za svaki $S = \{a_1, a_2, ... , a_k\} \subset \mathbb{N}$ takav da $i \neq j \implies a_i \neq a_j $ postoji beskonačno mnogo $n \in \mathbb{N}$ takvih da $\gcd(a_1 + n, a_2 + n, ..., a_k + n) = 1.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
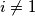
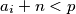
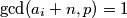
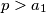
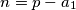
BSOMP da i da gdje je neki prost broj. Tada za svaki vrijedi pa time i . Budući da postoji beskonačno mnogo postoji i beskonačno mnogo takvih da ovo vrijedi.
%V0
BSOMP da $a_1 = \max(S)$ i da $a_1 + n = p$ gdje je $p$ neki prost broj. Tada za svaki $i \neq 1$ vrijedi $a_i + n < p$ pa time i $\gcd(a_i + n, p) = 1$. Budući da postoji beskonačno mnogo $p > a_1$ postoji i beskonačno mnogo $n = p - a_1$ takvih da ovo vrijedi.
Školjka 
takav da 
postoji beskonačno mnogo 
takvih da 
i da 
gdje je 
neki prost broj. Tada za svaki 
vrijedi 
pa time i 
. Budući da postoji beskonačno mnogo 
postoji i beskonačno mnogo 
takvih da ovo vrijedi.