Točno
4. siječnja 2016. 23:57 (10 godine, 2 mjeseci)
Dokaži da za svaki
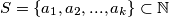
takav da
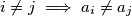
postoji beskonačno mnogo

takvih da
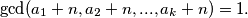
%V0
Dokaži da za svaki $S = \{a_1, a_2, ... , a_k\} \subset \mathbb{N}$ takav da $i \neq j \implies a_i \neq a_j $ postoji beskonačno mnogo $n \in \mathbb{N}$ takvih da $\gcd(a_1 + n, a_2 + n, ..., a_k + n) = 1.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je BSO
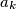
najveći od

-eva. Namjestimo

tako da je
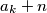
prost broj. Svi ostali
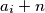
su manji od tog broja (i veći od jedan), pa ne mogu dijeliti faktor s tim brojem. Takvih dovoljno velikih prostih brojeva ima beskonačno, pa i

-ova ima beskonačno.
%V0
Neka je BSO $a_k$ najveći od $a_i$-eva. Namjestimo $n$ tako da je $a_k + n$ prost broj. Svi ostali $a_i + n$ su manji od tog broja (i veći od jedan), pa ne mogu dijeliti faktor s tim brojem. Takvih dovoljno velikih prostih brojeva ima beskonačno, pa i $n$-ova ima beskonačno.