Točno
12. siječnja 2016. 23:59 (8 godine, 10 mjeseci)
Pokažite da za svaka dva pozitivna broja
i
vrijedi nejednakost
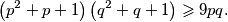
%V0
Pokažite da za svaka dva pozitivna broja $p$ i $q$ vrijedi nejednakost $$\left(p^2+p+1\right)\left(q^2+q+1\right) \geqslant 9pq \text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kako je
(p-1)^2>=0
<=> p^2 -2p +1 >=0
<=> p^2 + p +1 >=3p ; analogno slijedi da je q^2 + q + 1>=3q
Izmnožimo nejednakosti i dobit ćemo
(p^2 + p +1)(q^2 + q + 1) >=9pq
%V0
Kako je
(p-1)^2>=0
<=> p^2 -2p +1 >=0
<=> p^2 + p +1 >=3p ; analogno slijedi da je q^2 + q + 1>=3q
Izmnožimo nejednakosti i dobit ćemo
(p^2 + p +1)(q^2 + q + 1) >=9pq
| 13. siječnja 2016. 00:14 | matsimic | Točno |
| 19. siječnja 2016. 23:13 | grga | Točno |
Školjka