Točno
16. listopada 2015. 16:39 (10 godine, 4 mjeseci)
Let

,

,

,

,

,

be positive integers and let
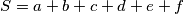
.
Suppose that the number

divides
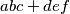
and
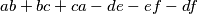
. Prove that

is composite.
%V0
Let $a$, $b$, $c$, $d$, $e$, $f$ be positive integers and let $S = a+b+c+d+e+f$.
Suppose that the number $S$ divides $abc+def$ and $ab+bc+ca-de-ef-df$. Prove that $S$ is composite.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo suprotno,

je prost.
Neka je
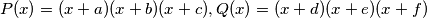
Iz pretpostavki zadatka vrijedi za svaki

cijeli broj:
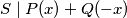
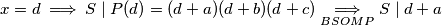
Sto je apsurdno jer
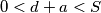
%V0
Pretpostavimo suprotno, $S$ je prost.
Neka je $P(x) = (x+a)(x+b)(x+c), Q(x) = (x+d)(x+e)(x+f)$
Iz pretpostavki zadatka vrijedi za svaki $x$ cijeli broj: $ S \mid P(x) + Q(-x)$
$x = d \implies S \mid P(d) = (d+a)(d+b)(d+c) \underset{BSOMP}{\implies} S \mid d+a $
Sto je apsurdno jer $0 < d+a < S$
| 28. listopada 2015. 13:42 | grga | Točno |