Točno
29. studenoga 2015. 19:49 (8 godine, 5 mjeseci)
Na uređeni par
možemo primjeniti sljedeće promjene:
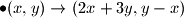
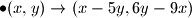
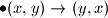
Poševši od para
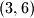
, možemo li dobiti
?
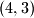
%V0
Na uređeni par $(x,y)$ možemo primjeniti sljedeće promjene:
$\bullet (x,y) \rightarrow (2x+3y,y-x)$
$\bullet (x,y) \rightarrow (x-5y,6y-9x)$
$\bullet (x,y) \rightarrow (y,x)$
Poševši od para $(3,6)$, možemo li dobiti $(4,3)$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Invarijanta: Ostatak pri dijeljenu zbroja obaju članova s 3.
Neka je
.
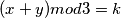
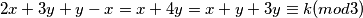
jer
.
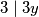
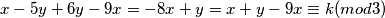
jer
.
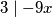
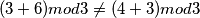
pa zadatak nije moguće izvršiti.
%V0
Invarijanta: Ostatak pri dijeljenu zbroja obaju članova s 3.
Neka je $(x+y) mod 3 = k$.
$2x+3y+y-x=x+4y=x+y+3y \equiv k (mod 3)$ jer $3 \mid 3y$.
$x-5y+6y-9x=-8x+y=x+y-9x \equiv k (mod 3)$ jer $3\mid-9x$.
$(3+6) mod 3 \neq (4+3) mod 3$ pa zadatak nije moguće izvršiti.
| 29. studenoga 2015. 22:07 | ikicic | Točno |
Školjka