Točno
3. svibnja 2016. 20:35 (9 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
pretpostavimo suprotno, da postoje takve  i
i 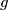 .
.
tada ocito postoji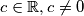 za koji
za koji 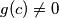 (inace bi npr. uvrstavanje
(inace bi npr. uvrstavanje 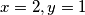 dovelo na kontradikciju).
dovelo na kontradikciju).
uvrstavajuci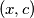 , nalazimo
, nalazimo
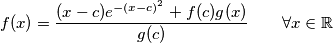
uvrstavajuci to nazad u pocetnu dobivamo
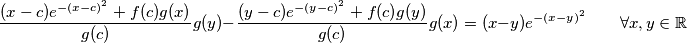
odnosno nakon mnozenja s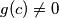 i sredivanja,
i sredivanja,
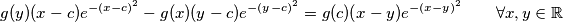
uvrstavajuci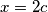 i
i 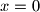 te izrazavajuci
te izrazavajuci 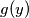 , zbog
, zbog 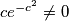 dobivamo
dobivamo
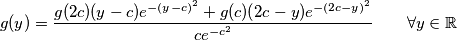
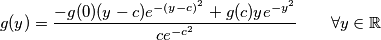
pa sada izjednacavanjem slijedi
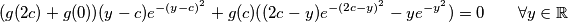
uvedimo supstituciju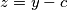 zbog simetrije. takoder, neka je
zbog simetrije. takoder, neka je 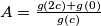 sto je opravdano zbog
sto je opravdano zbog 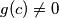 . prethodna jednakost postaje
. prethodna jednakost postaje
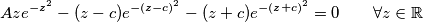
nekako je jasno da je vrlo tesko da ce ovaj identitet vrijediti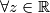 , ako je
, ako je 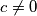 , ali pokazimo to. podijelimo sve s
, ali pokazimo to. podijelimo sve s 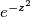 i s
i s 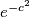 te oznacimo jos
te oznacimo jos 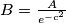 . takoder, neka je
. takoder, neka je 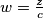 , te podijelimo sve s
, te podijelimo sve s  (opet, sve je opravdano zbog
(opet, sve je opravdano zbog 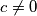 ). dobivamo
). dobivamo
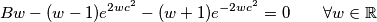
ako je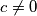 , tada je
, tada je 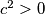 , pa ovo ne moze biti istina
, pa ovo ne moze biti istina 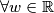 , jer za dovoljno velike
, jer za dovoljno velike  ,
, 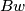 raste linearno a
raste linearno a 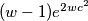 eksponencijalno, dok zadnji clan,
eksponencijalno, dok zadnji clan, 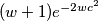 tezi u nulu, pa cijeli izraz tezi u
tezi u nulu, pa cijeli izraz tezi u 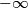 .
.
 i
i 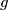 .
.tada ocito postoji
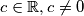 za koji
za koji 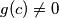 (inace bi npr. uvrstavanje
(inace bi npr. uvrstavanje 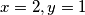 dovelo na kontradikciju).
dovelo na kontradikciju).uvrstavajuci
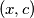 , nalazimo
, nalazimo 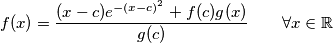
uvrstavajuci to nazad u pocetnu dobivamo
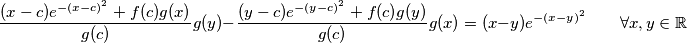
odnosno nakon mnozenja s
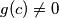 i sredivanja,
i sredivanja,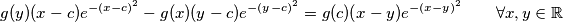
uvrstavajuci
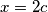 i
i 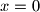 te izrazavajuci
te izrazavajuci 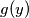 , zbog
, zbog 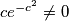 dobivamo
dobivamo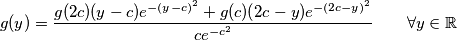
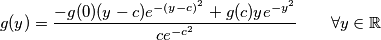
pa sada izjednacavanjem slijedi
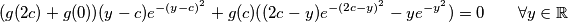
uvedimo supstituciju
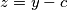 zbog simetrije. takoder, neka je
zbog simetrije. takoder, neka je 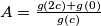 sto je opravdano zbog
sto je opravdano zbog 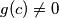 . prethodna jednakost postaje
. prethodna jednakost postaje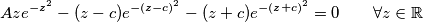
nekako je jasno da je vrlo tesko da ce ovaj identitet vrijediti
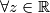 , ako je
, ako je 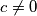 , ali pokazimo to. podijelimo sve s
, ali pokazimo to. podijelimo sve s 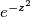 i s
i s 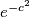 te oznacimo jos
te oznacimo jos 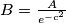 . takoder, neka je
. takoder, neka je 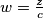 , te podijelimo sve s
, te podijelimo sve s  (opet, sve je opravdano zbog
(opet, sve je opravdano zbog 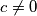 ). dobivamo
). dobivamo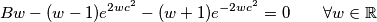
ako je
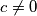 , tada je
, tada je 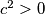 , pa ovo ne moze biti istina
, pa ovo ne moze biti istina 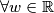 , jer za dovoljno velike
, jer za dovoljno velike  ,
, 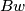 raste linearno a
raste linearno a 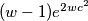 eksponencijalno, dok zadnji clan,
eksponencijalno, dok zadnji clan, 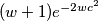 tezi u nulu, pa cijeli izraz tezi u
tezi u nulu, pa cijeli izraz tezi u 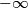 .
.  Školjka
Školjka 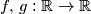 koje zadovoljavaju sljedeći izraz:
koje zadovoljavaju sljedeći izraz: 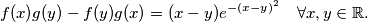
 fale koeficijenti
fale koeficijenti 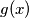 i
i