Točno
14. siječnja 2016. 10:45 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Označimo ∢BAD i ∢DCB sa α, a ∢CBA i ∢ADC sa β
Od prije znamo da je 2α + 2β = 360° => α + β = 180°
Simetrala dijeli kut α i stranicu CD na dva jednaka dijela.
Točkom M označimo sjecište simetrale i stranice CD te crtamo usporedni pravac NM sa stranicama AD i BC.
=> dobili smo 2 jednaka paralelograma, a svaki od njih krije po 2 trokuta tj. trokute AMD i ANM te trokute NBM i BCM.
Promatramo trokut AMD:
α/2 + |∢DMA| + β = 180°
Uvrstimo li prvu i drugu jednadžbu dobivamo izraz:
α + β = α/2 + |∢DMA| + β
=> α = 2|∢DMA| tj. α/2 = |∢DMA|
=> Trokuti AMD i ANM su jednakokračni
=> a/2 = b
=> Trokuti NBM i BCM su također jednakokračni.
Ako znamo da se kut dMC sastoji od 4 kutova 2 |∢AMN| i 2 |∢NMB| tada je njihov zbroj jednak 180° tj. vrijedi:
2 |∢AMN| + 2 |∢NMB| = 180°
=> |∢AMN| + |∢NMB| = 90°
Ako znamo da se kut ∢AMB sastoji od kutova |∢AMN| i |∢NMB|, tada znamo da je |∢AMB|=90°.
Od prije znamo da je 2α + 2β = 360° => α + β = 180°
Simetrala dijeli kut α i stranicu CD na dva jednaka dijela.
Točkom M označimo sjecište simetrale i stranice CD te crtamo usporedni pravac NM sa stranicama AD i BC.
=> dobili smo 2 jednaka paralelograma, a svaki od njih krije po 2 trokuta tj. trokute AMD i ANM te trokute NBM i BCM.
Promatramo trokut AMD:
α/2 + |∢DMA| + β = 180°
Uvrstimo li prvu i drugu jednadžbu dobivamo izraz:
α + β = α/2 + |∢DMA| + β
=> α = 2|∢DMA| tj. α/2 = |∢DMA|
=> Trokuti AMD i ANM su jednakokračni
=> a/2 = b
=> Trokuti NBM i BCM su također jednakokračni.
Ako znamo da se kut dMC sastoji od 4 kutova 2 |∢AMN| i 2 |∢NMB| tada je njihov zbroj jednak 180° tj. vrijedi:
2 |∢AMN| + 2 |∢NMB| = 180°
=> |∢AMN| + |∢NMB| = 90°
Ako znamo da se kut ∢AMB sastoji od kutova |∢AMN| i |∢NMB|, tada znamo da je |∢AMB|=90°.
Ocjene: (1)
Komentari:
ikicic, 12. siječnja 2016. 16:20
 Školjka
Školjka  simetrala kuta
simetrala kuta 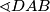 raspolavlja dužinu
raspolavlja dužinu  . Ako sa
. Ako sa  označimo polovište dužine
označimo polovište dužine 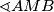 .
.