Točno
14. siječnja 2016. 21:41 (10 godine)
Nađite sve realne brojeve
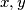
za koje vrijedi
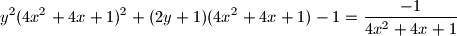
%V0
Nađite sve realne brojeve $x,y$ za koje vrijedi
$$y^2(4x^2+4x+1)^2+(2y+1)(4x^2+4x+1)-1=\frac{-1}{4x^2+4x+1}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Jednakost se može zapisati kao:
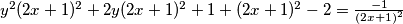
Odnosno nakon svođenja na kvadrat binoma na lijevoj strani i prebacivanja ostalog u razlomak na desnoj:
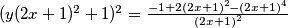
Prepoznajemo kvadrat binoma u brojniku:
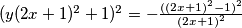
Iz zadatka imamo uvjet
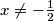
i slobodno možemo množiti cijelu jednakost s
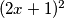
:
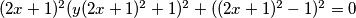
Sada dobivamo
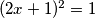
i
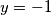
pa su rješenja dane jednadžbe
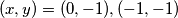
.
%V0
Jednakost se može zapisati kao:
$y^2(2x+1)^2+2y(2x+1)^2+1+(2x+1)^2-2=\frac{-1}{(2x+1)^2}$
Odnosno nakon svođenja na kvadrat binoma na lijevoj strani i prebacivanja ostalog u razlomak na desnoj:
$(y(2x+1)^2+1)^2=\frac{-1+2(2x+1)^2-(2x+1)^4}{(2x+1)^2}$
Prepoznajemo kvadrat binoma u brojniku:
$(y(2x+1)^2+1)^2=-\frac{((2x+1)^2-1)^2}{(2x+1)^2}$
Iz zadatka imamo uvjet $x\neq-\frac{1}{2}$ i slobodno možemo množiti cijelu jednakost s $(2x+1)^2$ :
$(2x+1)^2(y(2x+1)^2+1)^2+((2x+1)^2-1)^2=0$
Sada dobivamo $(2x+1)^2=1$ i $y=-1$ pa su rješenja dane jednadžbe $(x, y)=(0,-1), (-1,-1)$ .
| 15. siječnja 2016. 01:53 | ikicic | Točno |
| 19. siječnja 2016. 23:15 | grga | Točno |