Točno
17. siječnja 2016. 18:34 (10 godine, 1 mjesec)
Ako su

,

,

pozitivni realni brojevi takvi da je
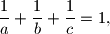
dokažite nejednakost
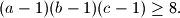
%V0
Ako su $a$, $b$, $c$ pozitivni realni brojevi takvi da je $$
\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=1,
$$ dokažite nejednakost $$
(a-1)(b-1)(c-1)\geq 8.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
(a-1)(b-1)(c-1)>=8
<=> abc-ac-bc-ab+a+b+c-1>=8, a iz uvjeta imamo da je ab + bc+ ac = abc
<=>a+b+c>=9
Primjenimo A-H
(a+b+c)/3 >= 3/(1/a +1/b +1/c) <=> (a+b+c)/3>=3 <=> a+b+c>=9
%V0
(a-1)(b-1)(c-1)>=8
<=> abc-ac-bc-ab+a+b+c-1>=8, a iz uvjeta imamo da je ab + bc+ ac = abc
<=>a+b+c>=9
Primjenimo A-H
(a+b+c)/3 >= 3/(1/a +1/b +1/c) <=> (a+b+c)/3>=3 <=> a+b+c>=9
| 18. siječnja 2016. 19:30 | ikicic | Točno |