Točno
17. siječnja 2016. 20:04 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je  polovište
polovište  i
i  polovište
polovište  i
i  težište. Treba dokazati
težište. Treba dokazati 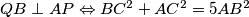 .
.
Dokažimo prvo smjer prema desno.
Neka je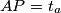 i
i 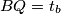 . Vrijedi
. Vrijedi 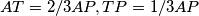 i analogno na
i analogno na 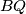 .
.
Po Pitagorinom poučku u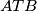 je
je 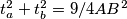 . U trokutima
. U trokutima 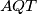 i
i 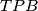 dobiva se redom
dobiva se redom 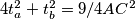 i
i 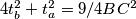 .
.
Zbrajanjem je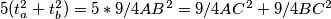 tj.
tj. 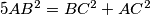 što je i trebalo dokazati.
što je i trebalo dokazati.
Drugi smjer:
Uvedimo oznake . Pretpostavljamo
. Pretpostavljamo 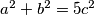 .
.
Opće je poznata formula za težišnicu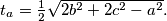 Tada je
Tada je 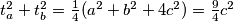 iz čega slijedi
iz čega slijedi 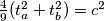 .
.
Po obratu Pitagorinog poučka je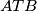 pravokutan odnosno
pravokutan odnosno 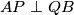 , što je i trebalo dokazati.
, što je i trebalo dokazati.
 polovište
polovište  i
i  polovište
polovište  i
i  težište. Treba dokazati
težište. Treba dokazati 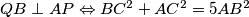 .
.Dokažimo prvo smjer prema desno.
Neka je
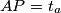 i
i 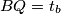 . Vrijedi
. Vrijedi 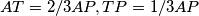 i analogno na
i analogno na 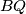 .
.Po Pitagorinom poučku u
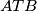 je
je 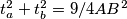 . U trokutima
. U trokutima 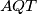 i
i 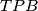 dobiva se redom
dobiva se redom 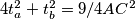 i
i 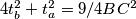 .
.Zbrajanjem je
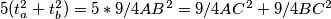 tj.
tj. 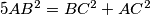 što je i trebalo dokazati.
što je i trebalo dokazati.Drugi smjer:
Uvedimo oznake
 . Pretpostavljamo
. Pretpostavljamo 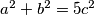 .
.Opće je poznata formula za težišnicu
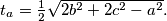 Tada je
Tada je 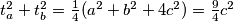 iz čega slijedi
iz čega slijedi 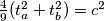 .
.Po obratu Pitagorinog poučka je
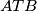 pravokutan odnosno
pravokutan odnosno 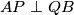 , što je i trebalo dokazati.
, što je i trebalo dokazati.  Školjka
Školjka  i
i  trokuta
trokuta  međusobno okomite ako i samo ako za duljine stranica vrijedi jednakost
međusobno okomite ako i samo ako za duljine stranica vrijedi jednakost