Točno
17. siječnja 2016. 21:45 (10 godine)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je zadani trokut  . Neka je
. Neka je 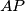 težišnica,
težišnica, 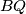 simetrala i
simetrala i 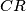 visina te
visina te 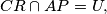
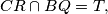
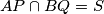 .
.
Pretpostavimo da je taj trokut doista jednakostraničan.
Tada je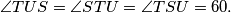
Možemo saznati vrijednosti kutova: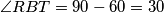 i dalje
i dalje 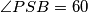
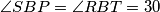 (simetrala) te je
(simetrala) te je 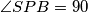 .
.
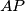 je po pretpostavci težišnica, ali i visina pa je trokut jednakokračan. Također ima kut
je po pretpostavci težišnica, ali i visina pa je trokut jednakokračan. Također ima kut 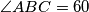 . Dakle trokut je jednakostraničan, ali tada bi se te dužine sjekle u jednoj točki, pa smo došli do kontradikcije.
. Dakle trokut je jednakostraničan, ali tada bi se te dužine sjekle u jednoj točki, pa smo došli do kontradikcije.
 . Neka je
. Neka je 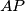 težišnica,
težišnica, 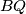 simetrala i
simetrala i 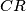 visina te
visina te 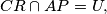
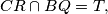
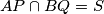 .
.Pretpostavimo da je taj trokut doista jednakostraničan.
Tada je
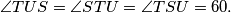
Možemo saznati vrijednosti kutova:
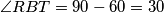 i dalje
i dalje 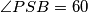
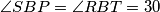 (simetrala) te je
(simetrala) te je 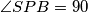 .
.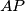 je po pretpostavci težišnica, ali i visina pa je trokut jednakokračan. Također ima kut
je po pretpostavci težišnica, ali i visina pa je trokut jednakokračan. Također ima kut 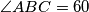 . Dakle trokut je jednakostraničan, ali tada bi se te dužine sjekle u jednoj točki, pa smo došli do kontradikcije.
. Dakle trokut je jednakostraničan, ali tada bi se te dužine sjekle u jednoj točki, pa smo došli do kontradikcije.  Školjka
Školjka