Točno
18. siječnja 2016. 01:11 (8 godine, 3 mjeseci)
Sakrij rješenje
Neka je
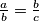
, gdje su
realni brojevi različiti od nule. Dokažite da tada vrijedi:
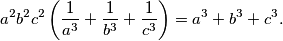
%V0
Neka je $\frac{a}{b}=\frac{b}{c}$, gdje su $a,b,c$ realni brojevi različiti od nule. Dokažite da tada vrijedi:
$$a^2b^2c^2\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)=a^3+b^3+c^3.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je
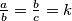
. Tada je
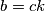
i
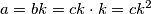
pa je
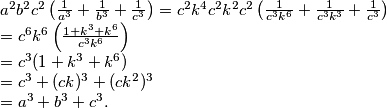
%V0
Neka je $\frac{a}{b}=\frac{b}{c}=k$. Tada je $b=ck$ i $a=bk=ck\cdot k=ck^2$ pa je
$
a^2b^2c^2\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right) =c^2k^4c^2k^2c^2\left(\frac{1}{c^3k^6}+\frac{1}{c^3k^3}+\frac{1}{c^3}\right)\\
=c^6k^6\left(\frac{1+k^3+k^6}{c^3k^6}\right)\\
=c^3(1+k^3+k^6)\\
=c^3+(ck)^3+(ck^2)^3\\
=a^3+b^3+c^3.
$
| 18. siječnja 2016. 13:29 | ikicic | Točno |
Školjka