Neocijenjeno
18. siječnja 2016. 01:12 (10 godine, 1 mjesec)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Označimo 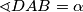 i
i 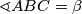 . Budući da je
. Budući da je  paralelogram, znamo da vrijedi
paralelogram, znamo da vrijedi 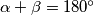 . Prema pretpostavci zadatka je
. Prema pretpostavci zadatka je 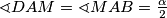 i
i 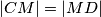 . No, vrijedi
. No, vrijedi 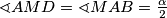 (jer su to kutovi uz presječnicu), pa je trokut
(jer su to kutovi uz presječnicu), pa je trokut 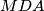 jednakokračan. Dakle,
jednakokračan. Dakle,
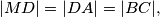
a odavde slijedi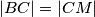 , tj. trokut
, tj. trokut 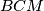 također je jednakokračan. Zbog toga imamo
također je jednakokračan. Zbog toga imamo 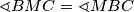 , a budući da također vrijedi
, a budući da također vrijedi 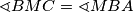 (jer su to kutovi uz presječnicu), slijedi
(jer su to kutovi uz presječnicu), slijedi 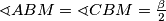 .\
.\
Konačno imamo
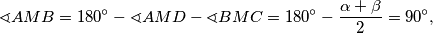
tj. kut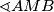 je pravi.
je pravi.
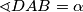 i
i 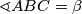 . Budući da je
. Budući da je  paralelogram, znamo da vrijedi
paralelogram, znamo da vrijedi 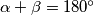 . Prema pretpostavci zadatka je
. Prema pretpostavci zadatka je 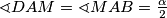 i
i 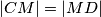 . No, vrijedi
. No, vrijedi 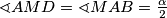 (jer su to kutovi uz presječnicu), pa je trokut
(jer su to kutovi uz presječnicu), pa je trokut 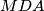 jednakokračan. Dakle,
jednakokračan. Dakle,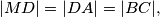
a odavde slijedi
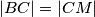 , tj. trokut
, tj. trokut 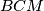 također je jednakokračan. Zbog toga imamo
također je jednakokračan. Zbog toga imamo 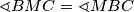 , a budući da također vrijedi
, a budući da također vrijedi 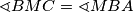 (jer su to kutovi uz presječnicu), slijedi
(jer su to kutovi uz presječnicu), slijedi 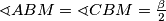 .\
.\Konačno imamo
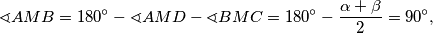
tj. kut
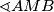 je pravi.
je pravi.  Školjka
Školjka 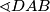 raspolavlja dužinu
raspolavlja dužinu  . Ako sa
. Ako sa  označimo polovište dužine
označimo polovište dužine