Točno
18. siječnja 2016. 01:12 (10 godine)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Budući da je ![x,y\in[a,b]](/media/m/1/0/e/10eecd0a7becb8f46e40e628617729df.png) , imamo
, imamo
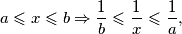
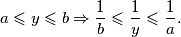
Zbrajanjem ovih nejednakosti dobivamo
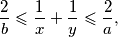
pa kako bi tvrdnja zadatka bila ispunjena, mora vrijediti
![\left[\frac{2}{b},\frac{2}{a}\right]\subseteq[a,b],](/media/m/b/f/4/bf4b65ac3f4afdcf56295a614b1816bc.png)
tj.
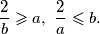
Množenjem ovih nejednakosti brojevima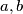 , tim redom (ti su brojevi prirodni pa se znak nejednakosti neće promijeniti), dobivamo
, tim redom (ti su brojevi prirodni pa se znak nejednakosti neće promijeniti), dobivamo
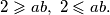
Dakle, mora biti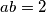 . Budući da su
. Budući da su  i
i  prirodni brojevi, vidimo da je jedino moguće rješenje
prirodni brojevi, vidimo da je jedino moguće rješenje 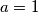 ,
,  .
.
![x,y\in[a,b]](/media/m/1/0/e/10eecd0a7becb8f46e40e628617729df.png) , imamo
, imamo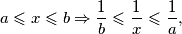
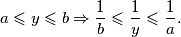
Zbrajanjem ovih nejednakosti dobivamo
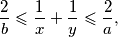
pa kako bi tvrdnja zadatka bila ispunjena, mora vrijediti
![\left[\frac{2}{b},\frac{2}{a}\right]\subseteq[a,b],](/media/m/b/f/4/bf4b65ac3f4afdcf56295a614b1816bc.png)
tj.
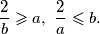
Množenjem ovih nejednakosti brojevima
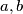 , tim redom (ti su brojevi prirodni pa se znak nejednakosti neće promijeniti), dobivamo
, tim redom (ti su brojevi prirodni pa se znak nejednakosti neće promijeniti), dobivamo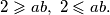
Dakle, mora biti
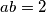 . Budući da su
. Budući da su  i
i  prirodni brojevi, vidimo da je jedino moguće rješenje
prirodni brojevi, vidimo da je jedino moguće rješenje 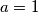 ,
,  .
.  Školjka
Školjka 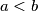 , takve da za sve realne brojeve
, takve da za sve realne brojeve ![\frac{1}{x}+\frac{1}{y}\in[a,b].](/media/m/c/3/1/c311e45b444da431a5bca5874bb927ef.png)