Točno
23. siječnja 2016. 18:59 (10 godine, 1 mjesec)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
(a) Uočimo da tvrdnju očito zadovoljava svaki prirodan broj koji nije prost i kojemu su svi prosti faktori veći od 2016. Budući da je 2017 prost broj, jedan takav broj je 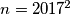 : njegov jedini prost faktor je 2017 i vrijedi
: njegov jedini prost faktor je 2017 i vrijedi
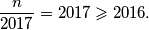
(b) Označimo sa traženi broj. Ako je
traženi broj. Ako je  djeljiv s 2, onda je prema pretpostavci zadatka
djeljiv s 2, onda je prema pretpostavci zadatka 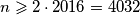 . Ukoliko je
. Ukoliko je  djeljiv i s 3, onda je
djeljiv i s 3, onda je 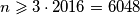 . Ukoliko sada pretpostavimo da se
. Ukoliko sada pretpostavimo da se  nalazi između ta dva broja (jer tražimo najmanji takav
nalazi između ta dva broja (jer tražimo najmanji takav  ), slijedi da
), slijedi da  može biti djeljiv jedino brojem 2, tj. da je
može biti djeljiv jedino brojem 2, tj. da je  potencija broja 2. Sada lako vidimo da je
potencija broja 2. Sada lako vidimo da je 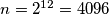 traženi broj.
traženi broj.
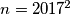 : njegov jedini prost faktor je 2017 i vrijedi
: njegov jedini prost faktor je 2017 i vrijedi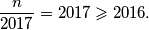
(b) Označimo sa
 traženi broj. Ako je
traženi broj. Ako je  djeljiv s 2, onda je prema pretpostavci zadatka
djeljiv s 2, onda je prema pretpostavci zadatka 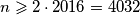 . Ukoliko je
. Ukoliko je  djeljiv i s 3, onda je
djeljiv i s 3, onda je 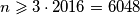 . Ukoliko sada pretpostavimo da se
. Ukoliko sada pretpostavimo da se  nalazi između ta dva broja (jer tražimo najmanji takav
nalazi između ta dva broja (jer tražimo najmanji takav  ), slijedi da
), slijedi da  može biti djeljiv jedino brojem 2, tj. da je
može biti djeljiv jedino brojem 2, tj. da je  potencija broja 2. Sada lako vidimo da je
potencija broja 2. Sada lako vidimo da je 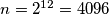 traženi broj.
traženi broj. Ocjene: (2)
Komentari:
grga, 23. siječnja 2016. 19:11
zadatak trazi najmanji broj koji je bar 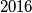 puta veci od svih svojih prostih faktora, a ne broj koji je za bar
puta veci od svih svojih prostih faktora, a ne broj koji je za bar 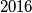 veci od svih svojih prostih faktora.
veci od svih svojih prostih faktora.
no, cak i kad bi zadatak bio naci broj koji je za bar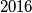 veci od svih svojih prostih faktora, nadam se da je iz konstrukcije sluzbenog rjesenja jasno da ce vec
veci od svih svojih prostih faktora, nadam se da je iz konstrukcije sluzbenog rjesenja jasno da ce vec 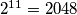 biti manji od broja kojeg si ti ponudio, a imati trazeno svojstvo. ipak, u ovom slucaju je odgovor
biti manji od broja kojeg si ti ponudio, a imati trazeno svojstvo. ipak, u ovom slucaju je odgovor 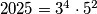 iako ne znam kako bih to rjesio osim ispisivanjem slucajeva.
iako ne znam kako bih to rjesio osim ispisivanjem slucajeva.
u svakom slucaju, dobar primjer krivog rjesenja, jer lijepo pokazuje kada ono sto nam se na prvu cini "optimalnom strategijom odabira naseg broja", tj u ovom slucaju biranje broja oblika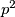 zapravo nije tocno rjesenje :)
zapravo nije tocno rjesenje :)
i, mislim da inace vrijedi ako je rjesenje oznaceno kao sluzbeno, ima manje sanse biti krivo nego ako nije (iskreno, ja nisam pisao ovo rjesenje, nego sam ga kopirao), pa mozda nije lose dvaput razmisliti jeli nesto ocito krivo. ali u svakom slucaju je pohvalno pokusati naci gresku u sluzbenom rjesenju! nebi bio ni prvi ni zadnji put da je potpuno krivo ;)
EDIT: hvala za "end description", to je bila jos jedna naznaka da sam copypasteo :P
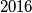 puta veci od svih svojih prostih faktora, a ne broj koji je za bar
puta veci od svih svojih prostih faktora, a ne broj koji je za bar 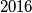 veci od svih svojih prostih faktora.
veci od svih svojih prostih faktora.no, cak i kad bi zadatak bio naci broj koji je za bar
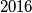 veci od svih svojih prostih faktora, nadam se da je iz konstrukcije sluzbenog rjesenja jasno da ce vec
veci od svih svojih prostih faktora, nadam se da je iz konstrukcije sluzbenog rjesenja jasno da ce vec 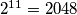 biti manji od broja kojeg si ti ponudio, a imati trazeno svojstvo. ipak, u ovom slucaju je odgovor
biti manji od broja kojeg si ti ponudio, a imati trazeno svojstvo. ipak, u ovom slucaju je odgovor 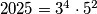 iako ne znam kako bih to rjesio osim ispisivanjem slucajeva.
iako ne znam kako bih to rjesio osim ispisivanjem slucajeva.u svakom slucaju, dobar primjer krivog rjesenja, jer lijepo pokazuje kada ono sto nam se na prvu cini "optimalnom strategijom odabira naseg broja", tj u ovom slucaju biranje broja oblika
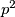 zapravo nije tocno rjesenje :)
zapravo nije tocno rjesenje :)i, mislim da inace vrijedi ako je rjesenje oznaceno kao sluzbeno, ima manje sanse biti krivo nego ako nije (iskreno, ja nisam pisao ovo rjesenje, nego sam ga kopirao), pa mozda nije lose dvaput razmisliti jeli nesto ocito krivo. ali u svakom slucaju je pohvalno pokusati naci gresku u sluzbenom rjesenju! nebi bio ni prvi ni zadnji put da je potpuno krivo ;)
EDIT: hvala za "end description", to je bila jos jedna naznaka da sam copypasteo :P
Zadnja promjena: grga, 23. siječnja 2016. 19:11
marin049, 22. siječnja 2016. 21:53
ikicic, 18. siječnja 2016. 13:32
 Školjka
Školjka 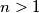 koji je barem 2016 puta veći od svakog od svojih prostih faktora,
koji je barem 2016 puta veći od svakog od svojih prostih faktora, prost. Sada je
prost. Sada je 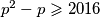 , tj.
, tj.  , prvi takav prosti broj je
, prvi takav prosti broj je 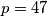 , pa je rezultat
, pa je rezultat